题目内容
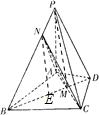
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M是AC的中点,PA=AB=4,且∠CAD=30°,点N在线段PB上,且
如图,四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M是AC的中点,PA=AB=4,且∠CAD=30°,点N在线段PB上,且| BN |
| NP |
(Ⅰ)求证:MN∥平面PDC;
(Ⅱ)求三棱锥N-PAC的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(I)通过证明线段成比例证明MN∥PD,利用直线 平面平行的判定定理证明MN∥平面PDC;
(II)连接PM,在△PBM中,过N作NE∥BM交PM于点E,由线面垂直的判定定理可得NE为三棱锥N-PAC的高,求出棱锥的底面积,代入棱锥体积公式,可得答案.
(II)连接PM,在△PBM中,过N作NE∥BM交PM于点E,由线面垂直的判定定理可得NE为三棱锥N-PAC的高,求出棱锥的底面积,代入棱锥体积公式,可得答案.
解答:
证明:(I)在正三角形ABC中,BM=2
,AC=AB=4,
在△ACD,因为M为AC中点,DM⊥AC,
所以AD=CD
∠CAD=30°,
所以,DM=
,
所以BM:MD=3:1,
所以BN:NP=BM:MD,
所以MN∥PD,
又MN?平面PDC,PD?平面PDC,
所以MN∥平面PDC;
解:(II)∵PA⊥平面ABCD,BM?平面ABCD,
∴PA⊥BM,
又由BM⊥AC,AC∩PA=A,AC,PA?平面PAC,
∴BM⊥平面PAC,
连接PM,在△PBM中,过N作NE∥BM交PM于点E,
则NE⊥平面PAC,即NE为三棱锥N-PAC的高,
∵BM=2
,且
=3.
∴NE=
BM=
,
又∵△PAC的面积S=
×4×4=8,
故三棱锥N-PAC的体积V=
×8×
=
| 3 |
在△ACD,因为M为AC中点,DM⊥AC,
所以AD=CD
∠CAD=30°,
所以,DM=
2
| ||
| 3 |
所以BM:MD=3:1,
所以BN:NP=BM:MD,
所以MN∥PD,
又MN?平面PDC,PD?平面PDC,
所以MN∥平面PDC;
解:(II)∵PA⊥平面ABCD,BM?平面ABCD,
∴PA⊥BM,
又由BM⊥AC,AC∩PA=A,AC,PA?平面PAC,
∴BM⊥平面PAC,

连接PM,在△PBM中,过N作NE∥BM交PM于点E,
则NE⊥平面PAC,即NE为三棱锥N-PAC的高,
∵BM=2
| 3 |
| BN |
| NP |
∴NE=
| 1 |
| 4 |
| ||
| 2 |
又∵△PAC的面积S=
| 1 |
| 2 |
故三棱锥N-PAC的体积V=
| 1 |
| 3 |
| ||
| 2 |
4
| ||
| 3 |
点评:本题考查的知识点是棱锥的体积,直线与平面平行的判定,直线与平面垂直的判定及性质,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示的几何体中,ABC-A1B1C1为正三棱柱,点D在底面ABC中,且DA=DC=AC=2,AA1=3,E为棱A1C1的中点.
如图所示的几何体中,ABC-A1B1C1为正三棱柱,点D在底面ABC中,且DA=DC=AC=2,AA1=3,E为棱A1C1的中点.