Question

已知点M（4，0），点P在曲线y²=8x上运动，点Q在曲线（x-2）²+y²=1上运动，则

|PM|2

|PQ|

的最小值是

 

．

Answer 1

考点：两点间距离公式的应用,轨迹方程

专题：圆锥曲线的定义、性质与方程

分析：设圆心为F，则容易知道F为抛物线y²=8x的焦点，并且

|PM|2

|PQ|

最小时，PM经过圆心F，设P（x，y），则：
|PM|²=（x-4）²+y²=（x-4）²+8x=x²+16，|PQ|=x+2+1=x+3，所以

|PM|2

|PQ|

=

x2+16

x+3

，求

x2+16

x+3

的最小值即可．

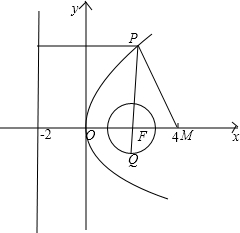
解答： 解：如下图，设圆心为F，则F为抛物线y²=8x的焦点，该抛物线的准线方程为x=-2，设P（x，y），由抛物线的定义：
|PF|=x+2，要使

|PM|2

|PQ|

最小，则|PQ|需最大，如图，|PQ|最大时，经过圆心F，且圆F的半径为1，∴|PQ|=|PF|+1=x+3，且|PM|=

(x-4)2+y2

=

(x-4)2+8x

=

x2+16

；
∴

|PM|2

|PQ|

=

x2+16

x+3

，令x+3=t（t≥3），则x=t-3，∴

|PM|2

|PQ|

=

(t-3)2+16

t

=t+

25

t

-6≥4，当t=5时取“=“；
∴

|PM|2

|PQ|

的最小值是4．
故答案为：4．

点评：考查抛物线的标准方程，焦点坐标公式，准线方程，及抛物线的定义，圆的标准方程，利用基本不等式：a+b≥2

ab

(a，b＞0)求函数的最值．