题目内容
已知函数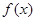 的定义域是
的定义域是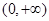 ,
,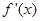 是
是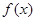 的导函数,且
的导函数,且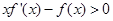 在
在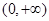 内恒成立.
内恒成立.
(1)求函数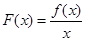 的单调区间;
的单调区间;
(2)若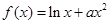 ,求
,求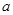 的取值范围;
的取值范围;
(3)设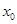 是
是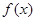 的零点,
的零点,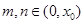 ,求证:
,求证: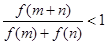
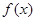 的定义域是
的定义域是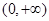 ,
,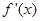 是
是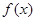 的导函数,且
的导函数,且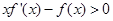 在
在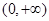 内恒成立.
内恒成立.(1)求函数
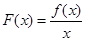 的单调区间;
的单调区间;(2)若
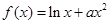 ,求
,求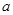 的取值范围;
的取值范围;(3)设
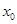 是
是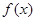 的零点,
的零点,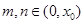 ,求证:
,求证: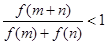
(1) 的单调区间为
的单调区间为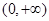 ;(2)
;(2) ;(3)利用函数的单调性及放缩法证明
;(3)利用函数的单调性及放缩法证明
 的单调区间为
的单调区间为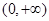 ;(2)
;(2) ;(3)利用函数的单调性及放缩法证明
;(3)利用函数的单调性及放缩法证明试题分析:(1)
 ,∵
,∵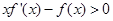 在
在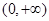 内恒成立
内恒成立∴
 在
在 内恒成立,∴
内恒成立,∴ 的单调区间为
的单调区间为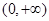 4分
4分(2)
 ,∵
,∵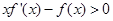 在
在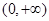 内恒成立
内恒成立∴
 在
在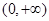 内恒成立,即
内恒成立,即 在
在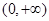 内恒成立,
内恒成立,设
 ,
,
 ,
, ,
, ,
, ,
,故函数
 在
在 内单调递增,在
内单调递增,在 内单调递减,
内单调递减,∴
 ,∴
,∴ 8分
8分(3)∵
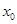 是
是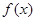 的零点,∴
的零点,∴ 由(1),
由(1), 在
在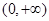 内单调递增,
内单调递增,∴当
 时,
时, ,即
,即 ,
,∴
 时
时 ,∵
,∵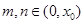 ,∴
,∴ ,
,且
 即
即
∴
 ,
,∴
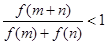 14分
14分点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点

练习册系列答案
相关题目
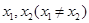 是函数
是函数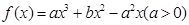 的两个极值点.
的两个极值点.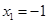 ,
,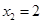 ,求函数
,求函数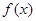 的解析式;
的解析式;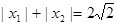 ,求实数
,求实数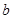 的最大值;
的最大值;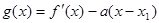 ,若
,若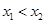 ,且
,且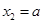 ,求函数
,求函数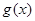 在
在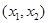 内的最小值.(用
内的最小值.(用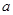 表示)
表示) ”是“可导函数
”是“可导函数 在点
在点 处取到极值”的 条件。 ( )
处取到极值”的 条件。 ( )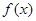 =
=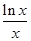 ,
,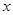 的不等式
的不等式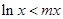 对一切
对一切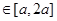 (其中
(其中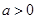 )都成立,求实数
)都成立,求实数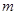 的取值范围;
的取值范围;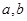
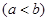 ,使
,使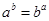 ?若不存在,说明理由;若存在,求
?若不存在,说明理由;若存在,求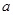 取值的范围
取值的范围
 在点
在点 处的切线斜率的最小值是( )
处的切线斜率的最小值是( ) 



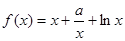 ,
,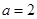 时,求函数
时,求函数 的单调增区间;
的单调增区间;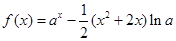 (
(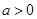 且
且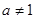 ).
).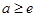 时,求证:
时,求证: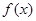 在
在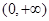 上单调递增;
上单调递增;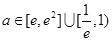 且
且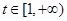 时,求证:
时,求证: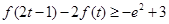 .
.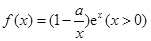 ,其中
,其中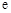 为自然对数的底数.
为自然对数的底数.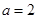 时,求曲线
时,求曲线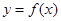 在
在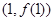 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;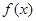 存在一个极大值和一个极小值,且极大值与极小值的积为
存在一个极大值和一个极小值,且极大值与极小值的积为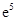 ,求
,求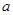 的
的