题目内容
已知f(x)=log3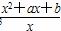 ,x∈(0,+∞),是否存在实数a,b,使f(x)同时满足下列条件:①在(0,1)上是减函数,在[1,+∞)上是增函数;②f(x)的最小值是1.若存在,求出a,b的值;若不存在,请说明理由.
,x∈(0,+∞),是否存在实数a,b,使f(x)同时满足下列条件:①在(0,1)上是减函数,在[1,+∞)上是增函数;②f(x)的最小值是1.若存在,求出a,b的值;若不存在,请说明理由.
假设存在实数a,b使命题成立,
∵f(x)在(0,1)上是减函数,在[1,+∞)上是增函数,
∴x=1时,f(x)取得最小值1,
∴log3 =1,∴a+b=2.
=1,∴a+b=2.
∵f(x)在(0,1)上是减函数,
设0<x1<x2<1,
∴f(x1)>f(x2)恒成立,
即 恒成立,
恒成立,
整理得 >0恒成立.
>0恒成立.
∵0<x1<x2<1,∴x1-x2<0,x1x2>0,
∴x1x2-b<0恒成立,即x1x2<b恒成立,
而x1x2<1,∴b≥1.
同理,f(x)在[1,+∞)上是增函数,
可得b≤1,∴b=1.又∵a+b=2,∴a=1.
故存在a=1,b=1同时满足题中条件.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 x,φ(x)=log2x,则f(
x,φ(x)=log2x,则f(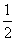 )+f(4)的值为________.
)+f(4)的值为________.
 的定义域是________.
的定义域是________.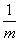 +
+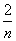 的最小值为( )
的最小值为( )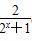 (x∈R).
(x∈R).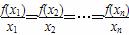 ,则n的取值范围为( )
,则n的取值范围为( )