题目内容
已知点A（1，2），B（-2，3），C（4，y）在同一条直线上，则y的值为（ ）
| A、-1 | ||
B、
| ||
| C、1 | ||
D、
|
考点：三点共线
专题：直线与圆
分析：根据三点共线，结合斜率之间的关系进行求解．
解答：
解：若点A（1，2），B（-2，3），C（4，y）在同一条直线上，
则满足kAB=kAC，
即
=
，
即-
=
，
则y-2=-1，解得y=1，
故选：C
则满足kAB=kAC，
即
| 3-2 |
| -2-1 |
| y-2 |
| 4-1 |
即-
| 1 |
| 3 |
| y-2 |
| 3 |
则y-2=-1，解得y=1，
故选：C
点评：本题主要考查三点共线的应用一件斜率公式的计算，根据斜率之间的关系是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知圆C1：（x-2）2+（y-3）2=1，圆C2：（x-3）2+（y-4）2=9，M，N分别是圆C1，C2上的动点，P为x轴上的动点，则|PM|+|PN|的最小值为（ ）
A、
| ||
B、5
| ||
C、6-2
| ||
D、
|
已知某地区中小学生人数和近视情况分别如图1和图2所示．为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为（ ）
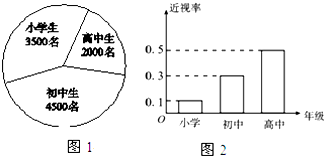
| A、200，20 |
| B、100，20 |
| C、200，10 |
| D、100，10 |