题目内容

16．若经过点（-4，a），（-2，6）的直线与直线x-2y-8=0垂直，则a的值为（　　）
A．$\frac{5}{2}$B．$\frac{2}{5}$C．10D．-10

分析 求两直线垂直与斜率之间的关系，建立方程，即可求得a的值．

解答 解：∵经过点（-4，a），（-2，6）的直线与直线x-2y-8=0垂直，
∴$\frac{6-a}{-2+4}$$•\frac{1}{2}$=-1，解得：a=10．
故选：C．

点评 本题考查了两直线垂直与斜率之间的关系，是基础的计算题．

练习册系列答案
相关题目
6．已知函数f（x）=|x-2|+|x+a|．
（1）若a=1，解不等式 f（x）≤2|x-2|；
（2）若f（x）≥2恒成立，求实数a的取值范围．
7．在△ABC中，角A，B，C所对的边分别是a，b，c，且满足cos2C-cos2A=2cos（$\frac{π}{6}$-C）cos（$\frac{π}{6}$+C）．
（1）求角A的大小；
（2）若A＜$\frac{π}{2}$，BC=$\sqrt{3}$，且sinA+sin（B-C）=2sin2C，求△ABC的面积．
4．已知函数f（x）=ex（ax2+bx+c）的导函数y=f′（x）的两个零点为-3和0．（其中e=2.71828…）
（Ⅰ）当a＞0时，求f（x）的单调区间；
（Ⅱ）若f（x）的极小值为-e3，求f（x）在区间[-5，1]上的最大值．
11．已知函数$f（x）=2sinxcosx+2\sqrt{3}{cos^2}x$．
（1）求函数f（x）的单调区间；
（2）当$x∈[{-\frac{π}{3}，\frac{π}{3}}]$时，求函数f（x）的最大值和最小值．
1．已知函数f（x）=x2+2x+a，g（x）=lnx-2x，如果存在${x_1}∈[{\frac{1}{2}，2}]$，使得对任意的${x_2}∈[{\frac{1}{2}，2}]$，都有f（x1）≤g（x2）成立，则实数a的取值范围是（-∞，ln2-$\frac{21}{4}$]．
8．已知向量$\overrightarrow{a}$=（-1，6），$\overrightarrow{b}$=（3，-2），则$\overrightarrow{a}$+$\overrightarrow{b}$=（　　）
A．（4，4）B．（2，4）C．（-2，4）D．（-4，4）
5．设相量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），若m$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$垂直，则实数m等于（　　）
A．-$\frac{6}{5}$B．$\frac{6}{5}$C．$\frac{9}{10}$D．-$\frac{9}{10}$
6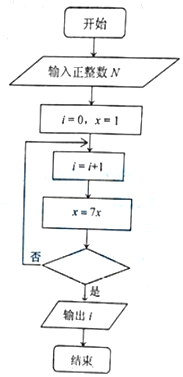．某同学为实现“给定正整数N，求最小的正整数i，使得7i＞N，”设计程序框图如右，则判断框中可填入（　　）
A．x≤NB．x＜NC．x＞ND．x≥N

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网