题目内容
如图,椭圆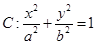 的顶点为
的顶点为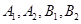 ,焦点为
,焦点为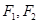 ,
,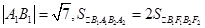 .
.
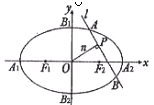
(Ⅰ)求椭圆C的方程;
(Ⅱ)设n 为过原点的直线,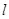 是与n垂直相交于P点,与椭圆相交于A, B两点的直线,
是与n垂直相交于P点,与椭圆相交于A, B两点的直线,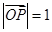 .是否存在上述直线
.是否存在上述直线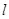 使
使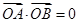 成立?若存在,求出直线
成立?若存在,求出直线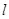 的方程;并说出;若不存在,请说明理由.
的方程;并说出;若不存在,请说明理由.
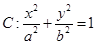 的顶点为
的顶点为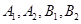 ,焦点为
,焦点为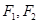 ,
,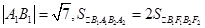 .
. 
(Ⅰ)求椭圆C的方程;
(Ⅱ)设n 为过原点的直线,
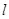 是与n垂直相交于P点,与椭圆相交于A, B两点的直线,
是与n垂直相交于P点,与椭圆相交于A, B两点的直线,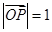 .是否存在上述直线
.是否存在上述直线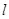 使
使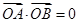 成立?若存在,求出直线
成立?若存在,求出直线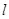 的方程;并说出;若不存在,请说明理由.
的方程;并说出;若不存在,请说明理由.(Ⅰ)  (Ⅱ)使
(Ⅱ)使 成立的直线
成立的直线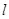 不存在.
不存在.
 (Ⅱ)使
(Ⅱ)使 成立的直线
成立的直线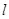 不存在.
不存在.试题分析:(Ⅰ)由
 知a2+b2=7, ①
知a2+b2=7, ①由
 知a=2c, ②
知a=2c, ②又b2=a2-c2 ③
由 ①,②,③解得a2=4,b2=3,
故椭圆C的方程为

(Ⅱ) 设A,B两点的坐标分别为

假设使
 成立的直线l存在,
成立的直线l存在,
(i) 当l不垂直于x轴时,设l的方程为
 ,
, 由l与n垂直相交于P点且
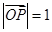 得
得 ,即m2=k2+1
,即m2=k2+1由
 得x1x2+y1y2=0
得x1x2+y1y2=0将y=kx+m代入椭圆方程,得(3+4k2)x2+8kmx+(4m2-12)=0,
由求根公式可得x1+x2=
 ④
④x1+x2=
 ⑤
⑤


将④,⑤代入上式并化简得
 ⑥
⑥将
 代入⑥并化简得
代入⑥并化简得 ,矛盾.
,矛盾.即此时直线
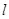 不存在.
不存在.(ii)当
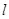 垂直于
垂直于 轴时,满足
轴时,满足 的直线
的直线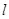 的方程为
的方程为 ,
,则A,B两点的坐标为
 或
或
当
 时,
时,
当
 时,
时,
∴ 此时直线
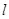 也不存在.
也不存在.综上可知,使
 成立的直线
成立的直线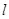 不存在.
不存在.点评:椭圆的概念和性质,仍将是今后命题的热点,定值、最值、范围问题将有所加强;利用直线、弦长、圆锥曲线三者的关系组成的各类试题是解析几何中长盛不衰的主题,其中求解与相交弦有关的综合题仍是今后命题的重点;与其它知识的交汇(如向量、不等式)命题将是今后高考命题的一个新的重点、热点.

练习册系列答案
相关题目
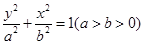 的上、下焦点,其中F1也是抛物线C2:
的上、下焦点,其中F1也是抛物线C2: 的焦点,点A是曲线C1,C2在第二象限的交点,且
的焦点,点A是曲线C1,C2在第二象限的交点,且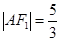

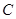 1的方程;
1的方程;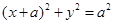 的直径,求
的直径,求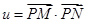 的最大值和最小值.
的最大值和最小值.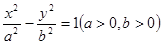 的左右焦点分别是
的左右焦点分别是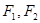 ,设
,设 是双曲线右支上一点,
是双曲线右支上一点, 在
在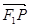 上投影的大小恰好为
上投影的大小恰好为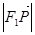 ,且它们的夹角为
,且它们的夹角为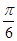 ,则双曲线的离心率为( )
,则双曲线的离心率为( )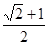

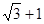
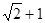
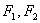 分别是椭圆的
分别是椭圆的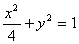 左,右焦点。
左,右焦点。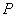 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且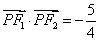 ,求点
,求点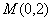 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点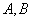 ,且
,且 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线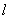 的斜率
的斜率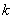 的取值范围。
的取值范围。 :
: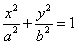 的离心率等于
的离心率等于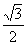 ,点
,点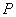
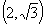 在椭圆上.
在椭圆上.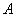 ,
,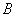 ,过点
,过点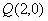 的动直线
的动直线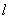 与椭圆
与椭圆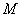 ,
,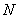 两点,是否存在定直线
两点,是否存在定直线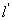 :
: ,使得
,使得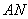 的交点
的交点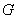 总在直线
总在直线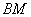 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的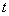 值;若不存在,说明理由。
值;若不存在,说明理由。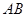 是过抛物线
是过抛物线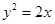 焦点的弦,
焦点的弦,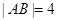 ,则
,则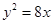 的焦点为右焦点,且经过点A(2,3).
的焦点为右焦点,且经过点A(2,3).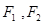 分别为椭圆的左右焦点,求
分别为椭圆的左右焦点,求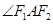 的角平分线所在直线的方程.
的角平分线所在直线的方程.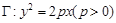 的焦点与椭圆
的焦点与椭圆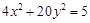 的右焦点重合.(Ⅰ)求抛物线
的右焦点重合.(Ⅰ)求抛物线 的方程;
的方程; 恒过点
恒过点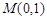 与抛物线
与抛物线 轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.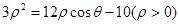
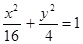 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值