题目内容
已知公差大于零的等差数列{an}的前n项和为Sn，且满足a3·a4＝117，a2＋a5＝
22.
(1)求通项an；
(2)若数列{bn}满足bn＝
，是否存在非零实数c使得{bn}为等差数列？若存在，求出c的值；若不存在，请说明理由．
解：(1)由等差数列的性质得，a2＋a5＝a3＋a4＝22，所以a3，a4是关于x的方程x2－22x＋117＝0的解，又公差大于零，所以a3＝9，a4＝13，易知a1＝1，d＝4，故通项为an＝1＋(n－1)×4＝
4n－3.
当n≥2时，bn－bn－1＝2.
故当c＝－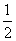
时，数列{bn}为等差数列．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
(x∈R)，有下列命题：
；
对称；
对称．
新架了一条索道AC，小李在山脚B处看索道，发现张角∠ABC＝120°，从B处攀登400米到达D处，回头看索道，发现张角∠ADC＝160°，从D处再攀登800米到达C处，问索道AC长多少？(精确到米，使用计算器计算) 
an－1，则满足
≤2的正整数n的集合为( )
＋b1＝7，a3＋b3＝21，则a5＋b5＝________.
，则a1a
a5＝________.
的前n项和Sn＝________.
0，则
的最小值是( )