Question

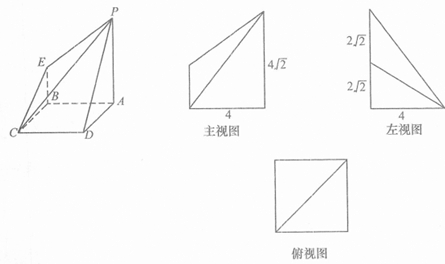
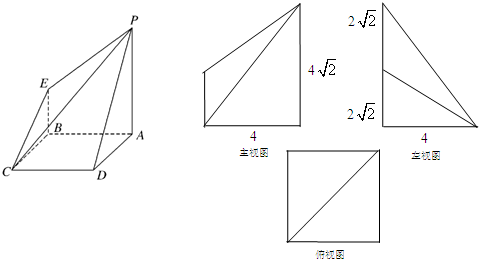
如图所示是一个几何体的三视图（单位：cm），主视图和左视图是底边长为4cm，腰长为2

2

的等腰三角形，俯视图是边长为4的正方形，则这个几何体的表面积是

16+16

2

．

Answer 1

分析：俯视图是正方形，且内部有两条相交的实线，说明原几何体有能够看到的侧棱，再结合主视图和左视图是两个全等的等腰三角形，还原得到原几何体是正四棱锥．

解答：解：由三视图可知原几何体是如图所示的正四棱锥
正四棱锥的底面边长AB=4，斜高PE=2

2

，
所以正四棱锥的表面积为四个侧面的面积加上底面积，
即S=4×

1

2

×AD×PE+AB×BC=4×

1

2

×4×2

2

+4×4=16+16

2

．
故答案为16+16

2

．

点评：本题考查了由三视图求原几何体的表面积，解答的关键是如何由几何体的三视图还原得到原几何体，由三视图得原几何体，首先分析俯视图，结合主视图和左视图得原图形，此题是中档题．