题目内容
(本小题满分14分)设函数 .
.
(1)若函数 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值;
(2)若存在 ,使
,使 成立,求正实数
成立,求正实数 的取值范围.
的取值范围.
(1) ;(2)
;(2)
【解析】
试题分析:(1)由已知得x>0,x≠1.
因f (x)在 上为减函数,故
上为减函数,故 在
在 上恒成立. 1分
上恒成立. 1分
所以当x∈ 时,
时, .
.
又 , 2分
, 2分
当 ,即
,即 时,
时, .
.
所以 于是
于是 ,故a的最小值为
,故a的最小值为 . 4分
. 4分
(2)命题“若存在 ,使
,使 成立”等价于“当
成立”等价于“当 时,有
时,有
 ”. 5分
”. 5分
由(Ⅰ),当 时,
时, ,∴
,∴ .
.
问题等价于:“当 时,有
时,有 ”. 6分
”. 6分
①当 时,由(1),
时,由(1), 在
在 上为减函数,
上为减函数,
则 ,故
,故 . 8分
. 8分
②当a< 时,由于
时,由于 在
在 上的值域为
上的值域为
(ⅰ) ,即
,即 ,
, 在
在 恒成立,故
恒成立,故 在
在 上为增函数,
上为增函数,
于是, ,矛盾. 10分
,矛盾. 10分
(ⅱ) ,即
,即 ,由
,由 的单调性和值域知,
的单调性和值域知,
存在唯一 ,使
,使 ,且满足:
,且满足:
当 时,
时, ,
, 为减函数;当
为减函数;当 时,
时, ,
, 为增函数;
为增函数;
所以, ,
, 12分
12分
所以, ,与
,与 矛盾. 13分
矛盾. 13分
综上,得 14分
14分
考点:本题考查利用导数研究函数的单调性,以及函数的最值

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,集合
,集合 ,则
,则 ( )
( )  B.
B. C.
C. D.
D.

 B.
B. C.
C. D.
D.
 上的奇函数
上的奇函数 ,当
,当 时,
时, ,则关于
,则关于 的函数
的函数 的所有零点之和为
的所有零点之和为 B.
B. C.
C. D.
D.
 的表达式是 ( )
的表达式是 ( ) B.
B.
 D.
D.
 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足
 的值;
的值; 且
且 ,求
,求 的取值范围.
的取值范围.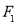 ,
,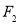 是双曲线
是双曲线 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点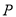 与点
与点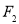 关于直线
关于直线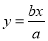 对称,则该双曲线的离心率为( )
对称,则该双曲线的离心率为( )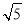 B.
B.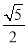 C.
C.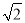 D.
D.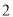
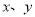 满足约束条件
满足约束条件 若目标函数
若目标函数 的最大值为7,则
的最大值为7,则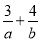 的最小值为_______.
的最小值为_______. ,
, 的最大值为2.
的最大值为2. 在
在 上的值域;
上的值域; 外接圆半径
外接圆半径 ,
, ,角
,角 所对的边分别是
所对的边分别是 ,求
,求 的值.
的值.