题目内容
定义在 上的奇函数
上的奇函数 ,当
,当 时,
时, ,则关于
,则关于 的函数
的函数 的所有零点之和为
的所有零点之和为
A. B.
B. C.
C. D.
D.
B
【解析】
试题分析: f(x)是连续奇函数,由以下6段分段函数组成:
(1)f(x)=-4-x x∈(-∞, -3],
(2)f(x)=x+2 x∈(-3, -1],
(3)f(x)=  x∈(-1, 0),
x∈(-1, 0),
(4)f(x)=  x∈[0, 1),
x∈[0, 1),
(5)f(x)=x-2 x∈[1, 3),
(6)f(x)=4-x x∈[3, +∞),
y=a(0<a<1)与 y=f(x)的第1,2,3,5,6 段分别有交点,
即 F(x)=f(x)-a 的零点.
其所有零点之和为
(-4-a)+(a-2)+(1-2^a)+(a+2)+(4-a)= 
考点:本题考查函数的图像和性质
点评:由奇函数的性质得到函数在 上的解析式,将函数的零点问题看做两个函数交点的问题处理
上的解析式,将函数的零点问题看做两个函数交点的问题处理

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 ,函数
,函数 ,若实数m,n满足f(m)>f(n),则m,n的大小关系为________.
,若实数m,n满足f(m)>f(n),则m,n的大小关系为________.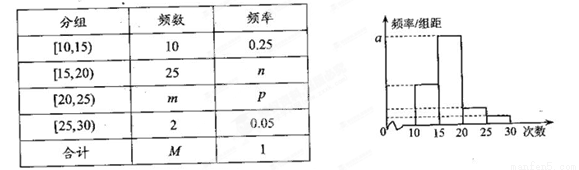
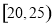 内的概率
内的概率 ,集合
,集合 (e是自然对数的底数),则
(e是自然对数的底数),则 ( )
( ) B.
B. C.
C. D.
D.
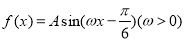 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是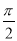 ,且满足,
,且满足, .
. 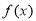 的单调递减区间;
的单调递减区间;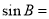
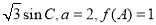 ,求△ABC的面积。
,求△ABC的面积。 ,
, ,曲线
,曲线 及
及 轴所围成的封闭图形的面积是( )
轴所围成的封闭图形的面积是( ) B.
B.
 D.
D.
 .
. 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值; ,使
,使 成立,求正实数
成立,求正实数