题目内容
3．已知正项数列{an}的前n项和为Sn，若{an}和{$\sqrt{{S}_{n}}$}都是等差数列，且公差相等，则a6=（ ）| A． | $\frac{11}{4}$ | B． | $\frac{3}{2}$ | C． | $\frac{7}{2}$ | D． | 1 |
分析 设等差数列{an}和{$\sqrt{{S}_{n}}$}的公差为d，可得an=a1+（n-1）d，$\sqrt{{S}_{n}}$=$\sqrt{{a}_{1}}$+（n-1）d，于是$\sqrt{{a}_{1}+{a}_{2}}$=$\sqrt{2{a}_{1}+d}$=$\sqrt{{a}_{1}}$+d，$\sqrt{3{a}_{1}+3d}$=$\sqrt{{a}_{1}}$+2d，化简整理可得：a1，d，即可得出．
解答 解：设等差数列{an}和{$\sqrt{{S}_{n}}$}的公差为d，
则an=a1+（n-1）d，$\sqrt{{S}_{n}}$=$\sqrt{{a}_{1}}$+（n-1）d，
∴$\sqrt{{a}_{1}+{a}_{2}}$=$\sqrt{2{a}_{1}+d}$=$\sqrt{{a}_{1}}$+d，$\sqrt{3{a}_{1}+3d}$=$\sqrt{{a}_{1}}$+2d，
平方化为：a1+d=d2+2$\sqrt{{a}_{1}}$d，2a1+3d=4d2+4$\sqrt{{a}_{1}}$d，
可得：a1=$2\sqrt{{a}_{1}}$d-d2，代入a1+d=d2+2$\sqrt{{a}_{1}}$d，
化为d（2d-1）=0，
解得d=0或$\frac{1}{2}$．
d=0时，可得a1=0，舍去．
∴$d=\frac{1}{2}$，a1=$\frac{1}{4}$．
∴a6=$\frac{1}{4}+\frac{1}{2}×5$=$\frac{11}{4}$．
故选：A．
点评 本题考查了等差数列的通项公式及其前n项和公式、递推关系、方程的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
8．已知函数f（x）=sin（2x+φ）（|φ|＜π）的图象过点P（0，$\frac{1}{2}$），如图，则φ的值为（ ）
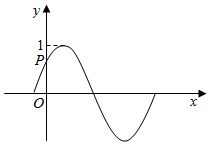
| A． | $\frac{π}{6}$ | B． | $\frac{5π}{6}$ | C． | $\frac{π}{6}$或$\frac{5π}{6}$ | D． | -$\frac{π}{6}$或$\frac{5π}{6}$ |
15．已知等差数列{an}，{bn}的前n项和分别是Sn，且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{3n-3}{2n+3}$，则$\frac{{a}_{6}}{{b}_{6}}$等于（ ）
| A． | $\frac{3}{2}$ | B． | 1 | C． | $\frac{6}{5}$ | D． | $\frac{27}{23}$ |