题目内容
15．已知cos2（α+$\frac{π}{4}$）=$\frac{1}{3}$，则sin2α=（ ）| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | -$\frac{2}{3}$ | D． | $\frac{2}{3}$ |
分析 由已知利用降幂公式，诱导公式即可化简求值得解．
解答 解：∵cos2（α+$\frac{π}{4}$）=$\frac{1+cos（2α+\frac{π}{2}）}{2}$=$\frac{1-sin2α}{2}$=$\frac{1}{3}$，
∴sin2α=$\frac{1}{3}$．
故选：B．
点评 本题主要考查了降幂公式，诱导公式在三角函数化简求值中的应用，考查了转化思想，属于基础题．
练习册系列答案
相关题目
6．已知i是虚数单位，则复数$\frac{2+i}{1-2i}$=（ ）
| A． | -i | B． | $\frac{4}{5}-\frac{3}{5}$i | C． | i | D． | $\frac{4}{3}$-i |
3．已知集合M={x|x2-x-2≤0}，N={y|y=2x}，则M∩N=（ ）
| A． | （0，2] | B． | （0，2） | C． | [0，2] | D． | [2，+∞） |
20．“k＞$-\frac{{\sqrt{3}}}{3}$”是“直线y=k（x+1）与圆（x-1）2+y2=1相交”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
4．两个函数的图象经过平移后能够重合，称这两个函数为“同形”函数，则下列四个函数：f1（x）=2log2（x+2），f2（x）=log2（x+2），f3（x）=log2（x+2）2，f4（x）=log22x，为“同形”函数的是（ ）
| A． | f1（x）与f3（x） | B． | f2（x）与f4（x） | C． | f1（x）与f2（x） | D． | f3（x）与f4（x） |
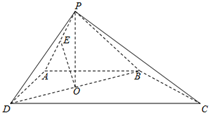如图，四棱锥P-ABCD的底面是直角梯形，AB∥CD，AB⊥AD，△PAB和△PAD是两个边长为2的正三角形，DC=4，O为BD的中点，E为PA的一动点．