题目内容
等差数列{an}中，a5=10，a12=31，则该数列的通项公式an= （n∈N+）
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：由已知条件利用等差数列的通项公式求出首项和公差，由此能求出该数列的通项公式．
解答：
解：∵等差数列{an}中，a5=10，a12=31，
∴
，
解得a1=-2，d=3，
∴an=-2+3（n-1）=3n-5．
故答案为：3n-5．
∴
|
解得a1=-2，d=3，
∴an=-2+3（n-1）=3n-5．
故答案为：3n-5．
点评：本题考查数列的通项公式的求法，是基础题，解题时要认真审题．
练习册系列答案
相关题目
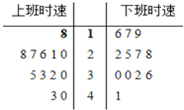某市对上下班交通情况作抽样调查，作出上下班时间各抽取的12辆机动车行驶时速（单位：km/h）的茎叶图如图．则上、下班行驶时速的中位数分别为（ ）| A、28与28.5 |
| B、29与28.5 |
| C、28与27.5 |
| D、29与27.5 |
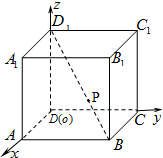如图在棱长为1正方体ABCD-A1B1C1D1中，以正方体的三条棱所在直线为轴建立空间直角坐标系Oxyz，