题目内容
【题目】已知圆![]() 的圆心
的圆心![]() 的坐标为
的坐标为![]() ,且圆
,且圆![]() 与直线
与直线![]() :
:![]() 相切,过点
相切,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)求![]() 的最小值;
的最小值;
(3)问:![]() 是否是定值?若是,求出这个定值;若不是,请说明理由.
是否是定值?若是,求出这个定值;若不是,请说明理由.
【答案】(1) ![]() . (2)
. (2) ![]() ; (3)
; (3) ![]() 是定值,定值为-10.
是定值,定值为-10.
【解析】
(1)根据圆![]() 与直线
与直线![]() :
:![]() 相切,即圆心到直线的距离等于半径,求出半径,即可写出圆
相切,即圆心到直线的距离等于半径,求出半径,即可写出圆![]() ;
;
(2)根据![]() 知当
知当![]() 为最大值
为最大值![]() 时,
时,![]() 有最小值;
有最小值;
(3)设![]() 中点为
中点为![]() ,
,![]() ,再设直线
,再设直线![]() ,联立方程组,计算即可得出
,联立方程组,计算即可得出![]() 。
。
解:(1)∵圆![]() 与直线
与直线![]() :
:![]() 相切,圆心为
相切,圆心为![]() ,
,
∴半径![]() ,
,
∴圆![]() 的方程为
的方程为![]() .
.
(2)∵![]() ,其中
,其中![]() 是圆心
是圆心![]() 到直线
到直线![]() 的距离,
的距离,
∴![]() 最大时,
最大时,![]() 最小.
最小.
∵当![]() 是弦
是弦![]() 中点时,
中点时,![]() 最大,且
最大,且![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.
(3)设![]() 中点为
中点为![]() ,则
,则![]() 即
即![]() ,∴
,∴![]() ,
,
且![]() ,
,
∴![]()
![]() .
.
当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() 方程为
方程为![]() ,代入圆
,代入圆![]() 方程得
方程得![]() ,
,
∴![]() 中点
中点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与直线
与直线![]() 的交点
的交点![]() 坐标为
坐标为![]() ,
,
∴![]() .∵
.∵![]() ,∴
,∴![]() ,
,
∴![]() ;
;
当![]() 与
与![]() 轴不垂直时,设
轴不垂直时,设![]() 方程为
方程为![]() ,
,
由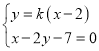 ,得
,得![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() ,
,
∴![]() 是定值,定值为-10.
是定值,定值为-10.

练习册系列答案
相关题目
【题目】下表是我省某地区2012年至2018年农村居民家庭年纯收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年纯收入 | 2 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2018年该地区农村居民家庭年纯收入的变化情况,并预测该地区2019年农村居民家庭年纯收入(结果精确到0.1)。
附:回归直线的斜率和截距的最小二乘法估计公式分别为: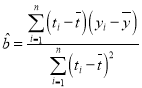 ,
,![]() 。
。