题目内容

计算
3
sin(-1200°)•tan
19π
6
-cos585°•tan(-
37π
4
)的值．
考点：运用诱导公式化简求值
专题：计算题,三角函数的求值
分析：利用诱导公式化简，结合特殊角的三角函数，即可求得结论．
解答： 解：原式=-
3
sin120°tan
π
6
+cos225°tan
π
4

=-
3
•
3
2
•
3
3
-
2
2
•1=-
3
+
2
2
．
点评：本题考查利用诱导公式化简，特殊角的三角函数，考查学生的计算能力，正确运用诱导公式化简是关键．
练习册系列答案
相关题目
设抛物线C：y2=2px（p＞0）的焦点为F，准线为l，M∈C，以M为圆心的圆M与l，相切于点Q，Q的纵坐标为
3
p，E（5，0）是圆M与x轴除F外的另一个交点
（Ⅰ）求抛物线C与圆M的方程：
（Ⅱ）过F且斜率为
4
3
的直线n与C交于A，B两点，求△ABQ的面积．
己知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点为F（1，0），点A（2，0）在椭圆C上，斜率为1的直线l与椭圆C交于不同两点M，N．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设直线过点F（1，0），求线段MN的长；
（Ⅲ）若直线l过点（m，0），且以MN为直径的圆恰过原点，求直线l的方程．
设双曲线C以椭圆
x2
25
+
y2
9
=1的两个焦点为焦点，且双曲线C的一条渐近线是y=
3
x．
（1）求双曲线C的方程；
（2）若直线y=kx+m（k≠0，m≠0）与双曲线C交于不同两点E，F，且E，F都在以P（0，3）为圆心的圆上，求实数m的取值范围．
已知函数y=5sin(5x+
π
6
)-1，
（1）写出函数的振幅、周期、初相；
（2）求函数的最大值和最小值并写出当函数取得最大值和最小值时x的相应取值．
已知命题p：“1≤x≤5是x2-（a+1）x+a≤0的充分不必要条件”，命题q：“满足AC=6，BC=a，∠CAB=30°的△ABC有两个”．若￢p∧q是真命题，求实数a的取值范围．
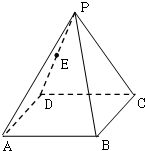如图，在各棱长都相等且底面为正方形的四棱锥P-ABCD中，E为PD的中点．
（1）画出过A、E两点且与直线DC平行的平面与四棱锥的截面，并证明你的画法是正确的；
（2）若（1）中截面与PC交于点F，求异面直线DC与AF所成角的大小．
已知函数f（log2x）=x-
1
x

（1）求f（x）的表达式；
（2）若不等式2tf（2t）+mf（t）≥0对于t∈[1，2]恒成立，求实数m的取值范围；
（3）若f（x）中，x=sinα+cosα，α∈（-
π
2
，0），且f（1-m）+f（1-m2）＜0，求实数m的取值范围．
设函数f（x）=x
x+2
，g（x）=
x+2
，则f（x）与g（x）的积F（x）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网