题目内容
13.已知函数f(x)=|lgx|,若0<a<b且f(a)=f(b),则a+2b的取值范围为(3,+∞).分析 画出函数f(x)的图象,则数形结合可知0<a<1,b>1,且ab=1,再将所求a+2b化为关于a的一元函数,利用函数单调性求函数的值域即可.
解答 解:画出y=|lgx|的图象如图:
∵0<a<b,且f(a)=f(b),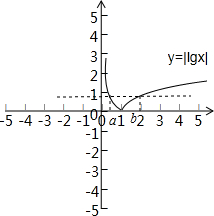
∴|lga|=|lgb|且0<a<1,b>1
∴-lga=lgb
即ab=1
∴y=a+2b=a+$\frac{2}{a}$,a∈(0,1)
∵y=a+$\frac{2}{a}$在(0,1)上为减函数,
∴y>1+2=3
∴a+2b的取值范围是(3,+∞)
故答案为:(3,+∞)
点评 本题主要考查了对数函数的图象和性质,利用“对勾”函数(或基本不等式)求函数值域的方法,数形结合的思想方法,转化化归的思想方法,难度中档.

练习册系列答案
相关题目
4.已知函数f(x)=|x-1|-1(x∈{0,1,2,3}),则其值域为( )
| A. | {0,1,2,3} | B. | {-1,0,1} | C. | {y|-1≤y≤1} | D. | {y|0≤y≤2} |
2.已知函数f(x)=a-x2(1≤x≤2)与g(x)=2x+1的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | [-2,-1] | B. | [-1,1] | C. | [1,3] | D. | [3,+∞] |
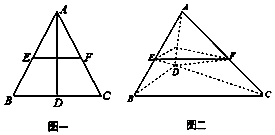 如图一,在边长为2的等边三角形ABC中,D、E、F分别是BC、AB、AC的中点,将△ABD沿AD折起,得到如图二所示的三棱锥A-BCD,其中$BC=\sqrt{2}$.
如图一,在边长为2的等边三角形ABC中,D、E、F分别是BC、AB、AC的中点,将△ABD沿AD折起,得到如图二所示的三棱锥A-BCD,其中$BC=\sqrt{2}$.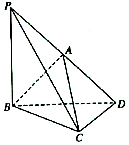 如图所示,在三棱锥A-BCD中,A在平面BCD内的投影恰为BD的中点,CD⊥BD,AD⊥AB,延长DA至P,使DA=AP.
如图所示,在三棱锥A-BCD中,A在平面BCD内的投影恰为BD的中点,CD⊥BD,AD⊥AB,延长DA至P,使DA=AP. 如图,点P为圆E:(x-1)2+y2=r2(r>1)与x轴的左交点,过点P作弦PQ,使PQ与y轴交于PQ的中点D.
如图,点P为圆E:(x-1)2+y2=r2(r>1)与x轴的左交点,过点P作弦PQ,使PQ与y轴交于PQ的中点D.