题目内容
5. 如图,点P为圆E:(x-1)2+y2=r2(r>1)与x轴的左交点,过点P作弦PQ,使PQ与y轴交于PQ的中点D.
如图,点P为圆E:(x-1)2+y2=r2(r>1)与x轴的左交点,过点P作弦PQ,使PQ与y轴交于PQ的中点D.(Ⅰ)当r在(1,+∞)内变化时,求点Q的轨迹方程;
(Ⅱ)已知点A(-1,1),设直线AQ,EQ分别与(Ⅰ)中的轨迹交于另一点Q1,Q2,求证:当Q在(Ⅰ)中的轨迹上移动时,只要Q1,Q2都存在,且Q1,Q2不重合,则直线Q1Q2恒过定点,并求该定点坐标.
分析 (Ⅰ)设Q(x,y),则PQ的中点$D(0,\frac{y}{2})$,由题意DE⊥DQ,得$\overrightarrow{DE}•\overrightarrow{DQ}=0$,代入坐标得答案;
(Ⅱ)分别设出Q、Q1、Q2的坐标,结合A,Q,Q1共线,E,Q,Q2共线可把Q1、Q2的坐标用Q的坐标表示,得到线Q1Q2的方程,再由直线系方程可得直线Q1Q2恒过定点,并求该定点坐标.
解答 (Ⅰ)解:设Q(x,y),则PQ的中点$D(0,\frac{y}{2})$,
∵E(1,0),∴$\overrightarrow{DE}=(1,-\frac{y}{2})$,$\overrightarrow{DQ}=(x,\frac{y}{2})$.
在圆E中,∵DE⊥DQ,∴$\overrightarrow{DE}•\overrightarrow{DQ}=0$,则$x-\frac{y^2}{4}=0$.
∴点Q的轨迹方程y2=4x(x≠0);
(Ⅱ)证明:设Q(t2,2t),${Q}_{1}({{t}_{1}}^{2},2{t}_{1})$,${Q}_{2}({{t}_{2}}^{2},2{t}_{2})$,
则直线Q1Q2的方程为(t1+t2)y-2x-2t1t2=0.
由A,Q,Q1共线,得$\frac{2{t}_{1}-2t}{{{t}_{1}}^{2}-{t}^{2}}=\frac{2t-1}{{t}^{2}+1}$,从而${t_1}=\frac{t+2}{2t-1}$($t≠\frac{1}{2}$,否则Q1不存在),
由E,Q,Q2共线,得$\frac{2{t}_{2}-2t}{{{t}_{2}}^{2}-{t}^{2}}=\frac{2t-0}{{t}^{2}-1}$,从而${t_2}=-\frac{1}{t}$(t≠0,否则Q2不存在),
∴${t_1}{t_2}=-\frac{t+2}{{2{t^2}-t}}$,${t_1}+{t_2}=\frac{{{t^2}+1}}{{2{t^2}-t}}$,
∴直线Q1Q2的方程化为t2(y-4x)+2t(x+1)+(y+4)=0,
令$\left\{\begin{array}{l}y-4x=0\\ x+1=0\\ y+4=0\end{array}\right.$,得x=-1,y=-4.
∴直线Q1Q2恒过定点(-1,-4).
点评 本题考查直线与抛物线位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,考查计算能力,属中档题.

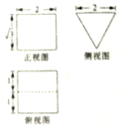
| A. | 20π | B. | $\frac{44}{3}$π | C. | $\frac{28}{3}$π | D. | 4π |
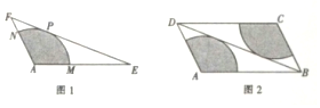
 如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).
如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2). 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和直线l:$\frac{x}{a}$-$\frac{y}{b}$=1,椭圆的离心率e=$\frac{\sqrt{6}}{3}$,坐标原点到直线l的距离为$\frac{\sqrt{3}}{2}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和直线l:$\frac{x}{a}$-$\frac{y}{b}$=1,椭圆的离心率e=$\frac{\sqrt{6}}{3}$,坐标原点到直线l的距离为$\frac{\sqrt{3}}{2}$.