题目内容
已知非零向量
,
和
满足(
+
)•
=0,且
=
,则△ABC的形状为 .
| AB |
| AC |
| BC |
| ||
|
|
| ||
|
|
| BC |
| ||||
|
|
| ||
| 2 |
考点:正弦定理
专题:解三角形,平面向量及应用
分析:先根据(
+
)•
=0判断出∠A的角平分线与BC垂直,进而推断三角形为等腰三角形进而根据向量的数量积公式求得C,判断出三角形的形状.
| ||
|
|
| ||
|
|
| BC |
解答:
解:∵(
+
)•
=0,
∴∠A的角平分线与BC垂直,
∴AB=AC,
∵cosC=
=
,
∴∠C=
,
∴∠A=
.
∴三角形为等腰直角三角形,
故答案为:等腰直角三角形.
| ||
|
|
| ||
|
|
| BC |
∴∠A的角平分线与BC垂直,
∴AB=AC,
∵cosC=
| ||||
|
|
| ||
| 2 |
∴∠C=
| π |
| 4 |
∴∠A=
| π |
| 2 |
∴三角形为等腰直角三角形,
故答案为:等腰直角三角形.
点评:本题主要考查了平面向量的数量积的运算,三角形形状的判断.考查了学生综合分析能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知i是虚数单位,z=1+i,
为z的共轭复数,则复数
在复平面上对应的点的坐标为( )
. |
| z |
| z2 | ||
|
| A、(1,1) |
| B、(-1,-1) |
| C、(-1,1) |
| D、(1,-1) |
设a,b,c∈R,且a>b,则( )
| A、a2>b2 | ||||
B、
| ||||
| C、lga>lgb | ||||
| D、2-a<2-b |
对于曲线y=ae
,令μ=lny,c=lna,v=
,可变换为线性回归模型,其形式为( )
| b |
| x |
| 1 |
| x |
| A、y=a+bv |
| B、μ=a+bv |
| C、μ=c+bv |
| D、y=c+bx |
已知双曲线C:
-
=1(a>0,b>0)的一条渐近方程为y=
x,则C的离心率为( )
| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
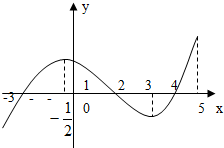 如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断: