题目内容
函数 在
在 上单调递增,则
上单调递增,则 的最小值为( )
的最小值为( )
| A.1 | B.3 | C.4 | D.9 |
B
解析试题分析:由题意f'(x)=ax2+bx+c≥0在R上恒成立,则a>0,△=b2-4ac≤0.∴ =
= ,令t=
,令t= (t>1),
(t>1), ≥
≥ =
= ≥3.(当且仅当t=4,即b=4a=4c时取“=”),故选B
≥3.(当且仅当t=4,即b=4a=4c时取“=”),故选B
考点:本题考查了导数的运用
点评:利用导数工具研究三次函数的单调性以及函数与方程的综合应用问题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
要做一个圆锥形漏斗,其母线长为20厘米,要使其体积最大,则其高应为( )厘米
A.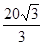 | B.100 | C.20 | D.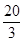 |
若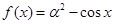 ,则
,则 等于( )
等于( )
A.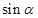 | B. | C.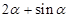 | D. |
由曲线 与直线
与直线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A. | B. | C. | D. |
曲线 在P点处的切线平行于直线
在P点处的切线平行于直线 ,则此切线方程是( )
,则此切线方程是( )
A. | B. |
C. | D. |
关于 的函数
的函数 的极值点的个数有( )
的极值点的个数有( )
| A.2个 | B.1个 | C.0个 | D.由 确定 确定 |
若函数 的导函数
的导函数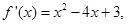 则函数
则函数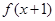 的单调递减区间是( )
的单调递减区间是( )
A.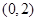 | B.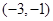 | C.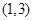 | D.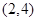 |
已知函数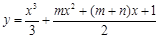 的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数
的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数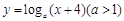 的图象上存在区域D内的点,则实数a的取值范围为( )
的图象上存在区域D内的点,则实数a的取值范围为( )
A.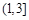 | B.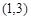 | C. | D.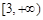 |
已知函数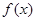 是定义在
是定义在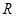 上的可导函数,且
上的可导函数,且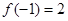 ,
, ,则不等式
,则不等式 的解集为
的解集为
A.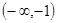 | B. | C. | D. |