题目内容
已知函数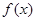 是定义在
是定义在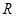 上的可导函数,且
上的可导函数,且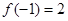 ,
, ,则不等式
,则不等式 的解集为
的解集为
A.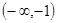 | B. | C. | D. |
B
解析试题分析:令 ,
, ,所以
,所以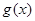 单调递增,而
单调递增,而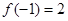 ,所以
,所以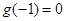 ,所以
,所以 等价于
等价于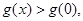 所以解集为
所以解集为 .
.
考点:本小题主要考查利用导数考查函数的单调性进而解抽象不等式.
点评:解决本小题的关键是构造新函数,进而考查函数的单调性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数 在
在 上单调递增,则
上单调递增,则 的最小值为( )
的最小值为( )
| A.1 | B.3 | C.4 | D.9 |
曲线 在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A. | B. | C. | D. |
已知实数a,b满足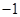 ≤a≤1,
≤a≤1,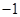 ≤b≤1,则函数
≤b≤1,则函数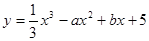 有极值的概率为( )
有极值的概率为( )
A. | B. | C.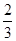 | D.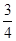 |
已知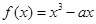 在
在 上递增,则
上递增,则 的范围是( )
的范围是( )
A.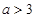 | B. | C.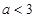 | D.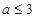 |
设曲线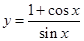 在点
在点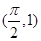 处的切线与直线
处的切线与直线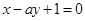 平行,则实数
平行,则实数 等于( )
等于( )
A.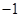 | B.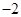 | C.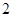 | D.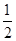 |
已知 ,且
,且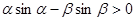 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A.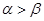 | B.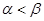 |
C.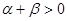 | D.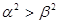 |
函数 的的单调递增区间是 ( )
的的单调递增区间是 ( )
A.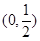 | B.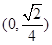 | C.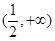 | D. 和 和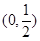 |
求曲线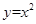 与
与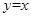 所围成图象的面积,其中正确的是( )
所围成图象的面积,其中正确的是( )
A.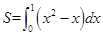 | B.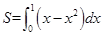 |
C.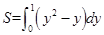 | D.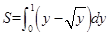 |