题目内容
由曲线 与直线
与直线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A. | B. | C. | D. |
D
解析试题分析:先确定交点坐标,得到积分区间,确定被积函数,求出原函数,即可求得结论.解:由题意,曲线y=x2-2x与直线x+y=0的交点坐标为(0,0),(1,-1),∴曲线y=x2-2x与直线x+y=0所围成的封闭图形的面积为S= ,故选D
,故选D
考点:定积分
点评:本题考查定积分知识的运用,确定交点坐标,得到积分区间,确定被积函数,是解题的关键.

练习册系列答案
相关题目
由曲线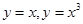 围成的封闭图形面积为[ ]
围成的封闭图形面积为[ ]
A.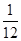 | B.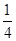 | C.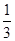 | D.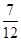 |
若 ,则
,则 等于( )
等于( )
A. | B. | C.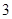 | D. |
已知曲线 在点
在点 处的切线经过点
处的切线经过点 ,则
,则 的值为
的值为
A. | B.1 | C.e | D.10 |
设 ,则二项式
,则二项式 的展开式中
的展开式中 项的系数为( )
项的系数为( )
| A.-192 | B.193 | C.-6 | D.7 |
函数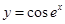 的导数是( )
的导数是( )
A.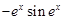 | B.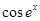 | C.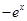 | D.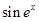 |
函数 在
在 上单调递增,则
上单调递增,则 的最小值为( )
的最小值为( )
| A.1 | B.3 | C.4 | D.9 |
已知函数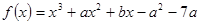 在
在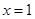 处取得极大值
处取得极大值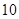 ,则
,则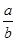 的值为( )
的值为( )
A. | B.-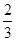 | C.-2或一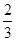 | D.不存在 |
已知实数a,b满足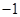 ≤a≤1,
≤a≤1,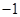 ≤b≤1,则函数
≤b≤1,则函数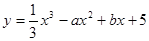 有极值的概率为( )
有极值的概率为( )
A. | B. | C.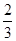 | D.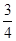 |