题目内容
要做一个圆锥形漏斗,其母线长为20厘米,要使其体积最大,则其高应为( )厘米
A.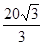 | B.100 | C.20 | D.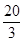 |
A
解析试题分析:设圆锥的高为h,则底面半径为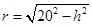 ,
,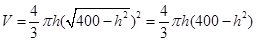 ,由
,由 得,h=
得,h=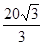 ,而这是唯一一个驻点,故高为
,而这是唯一一个驻点,故高为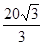 厘米时,体积最大,选D。
厘米时,体积最大,选D。
考点:圆锥的几何特征及体积计算,利用导数研究函数的最值。
点评:中档题,圆锥中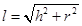 ,
, 。
。

练习册系列答案
相关题目
已知常数 、
、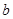 、
、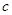 都是实数,
都是实数,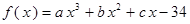 的导函数为
的导函数为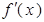 ,
,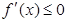 的解集为
的解集为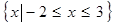 ,若
,若 的极小值等于
的极小值等于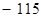 ,则
,则 的值是( )
的值是( )
A. | B.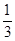 |
C.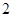 | D.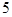 |
曲线 在点
在点 处的切线方程是
处的切线方程是
A. | B. | C. | D. |
由曲线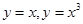 围成的封闭图形面积为[ ]
围成的封闭图形面积为[ ]
A.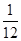 | B.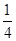 | C.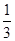 | D.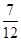 |
若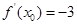 ,则
,则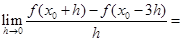 ( )
( )
A.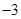 | B.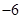 | C.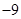 | D.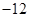 |
设 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时, ,且g(-3)=0,则不等式
,且g(-3)=0,则不等式 的解集是 ( )
的解集是 ( )
| A.(-3,0)∪(3,+∞) | B. (-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
若 ,则
,则 等于( )
等于( )
A. | B. | C.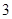 | D. |
函数 在
在 上单调递增,则
上单调递增,则 的最小值为( )
的最小值为( )
| A.1 | B.3 | C.4 | D.9 |
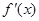 是函数f(x)的导函数,如果
是函数f(x)的导函数,如果
 ,那么曲线f(x)上任一点处的切线的倾斜角
,那么曲线f(x)上任一点处的切线的倾斜角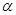 的取值范围是
的取值范围是