题目内容
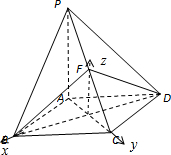
 如图,已知四棱锥P-ABCD的底面ABCD是菱形,PA=AD=AC=2,PD=
如图,已知四棱锥P-ABCD的底面ABCD是菱形,PA=AD=AC=2,PD=| 2 |
(1)求证:PA∥平面BFD;
(2)求二面角C-BF-D的余弦值;
(3)求三棱锥B-CDF的体积.
考点:棱柱、棱锥、棱台的体积,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)设AC∩BD=O,显然OF是三角形△PAC的中位线,可得PA∥OF,即可证明:PA∥平面BFD;
(2)建立空间直角坐标系,求出平面BFD、平面BFC的一个法向量,利用向量的夹角公式求二面角C-BF-D的余弦值;
(3)利用等体积转换求三棱锥B-CDF的体积.
(2)建立空间直角坐标系,求出平面BFD、平面BFC的一个法向量,利用向量的夹角公式求二面角C-BF-D的余弦值;
(3)利用等体积转换求三棱锥B-CDF的体积.
解答:
(1)证明:由已知,PD=PC=
PA,PA=AD=AC=2,
∴∠PAD=∠PAC=90°,即PA⊥AD,PA⊥AC.
又∵AD∩AC=A,
∴PA⊥平面ABCD.
设AC∩BD=O,显然OF是三角形△PAC的中位线,
∴PA∥OF,
又∵PA?平面BFD,OF?平面BFD,
∴PA∥平面BFD.…(4分)
(2)解:由(1)可知OF⊥平面ABCD,故不妨以O为原点,如图建立空间直角坐标系.
则
=(0,1,0),
=(-
,1,0),
=(-
,0,1),
且
是平面BFD的一个法向量.…(5分)
设平面BFC的一个法向量为
=(x,y,z),则
⇒
令z=
⇒
∴
=(1,
,
)…(7分)
设二面角C-BF-D的大小为θ,则cosθ=
=
=
∴二面角C-BF-D的余弦值为
.…(9分)
(3)解:∵S△BCD=
BD•OC=
×2
×1=
,OF⊥平面ABCD…(11分)
∴VB-CDF=VF-BCD=
•S△BCD•OF=
×
×1=
.…(13分)
| 2 |
∴∠PAD=∠PAC=90°,即PA⊥AD,PA⊥AC.
又∵AD∩AC=A,
∴PA⊥平面ABCD.
设AC∩BD=O,显然OF是三角形△PAC的中位线,
∴PA∥OF,
又∵PA?平面BFD,OF?平面BFD,
∴PA∥平面BFD.…(4分)
(2)解:由(1)可知OF⊥平面ABCD,故不妨以O为原点,如图建立空间直角坐标系.
则
| OC |
| BC |
| 3 |
| BF |
| 3 |

且
| OC |
设平面BFC的一个法向量为
| u |
|
|
| 3 |
|
∴
| u |
| 3 |
| 3 |
设二面角C-BF-D的大小为θ,则cosθ=
| ||||
|
|
| ||
1×
|
| ||
| 7 |
∴二面角C-BF-D的余弦值为
| ||
| 7 |
(3)解:∵S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴VB-CDF=VF-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| ||
| 3 |
点评:本题考查线面平行、垂直的判定,考查锥体体积的计算,考查学生分析解决问题的能力,正确运用线面平行、垂直的判定是关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目