题目内容

8．已知0≤x≤y≤1，则（2x-y）（1-2x）的最大值为$\frac{1}{8}$．

分析 0≤x≤y≤1，只考虑0≤x≤y≤2x≤1，则（2x-y）（1-2x）≤（2x-x）（1-2x）=$\frac{1}{2}×2x$（1-2x），再利用基本不等式的性质即可得出．

解答 解：∵0≤x≤y≤1，
只考虑0≤x≤y≤2x≤1，
则（2x-y）（1-2x）≤（2x-x）（1-2x）=$\frac{1}{2}×2x$（1-2x）≤$\frac{1}{2}（\frac{2x+1-2x}{2}）^{2}$=$\frac{1}{8}$，当且仅当2x=1-2x，x=$\frac{1}{4}$=y时取等号．
故答案为：$\frac{1}{8}$．

点评 本题考查了基本不等式的性质、不等式的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
18．已知函数$f（x）=2sin（2x-\frac{π}{3}）+1$
（Ⅰ）求f（x）的最小正周期、最值．
（Ⅱ）若对任意的x1，x2∈[0，$\frac{π}{2}$]，都有|f（x1）-f（x2）|＜m，求实数m的取值范围．
19．若曲线y=$\sqrt{|{x}^{2}-4|}$与直线y=x+m恰好有两个交点，则实数m的取值范围是（-2，0）∪{2}∪{$2\sqrt{2}$}．
16．甲、乙两人同时参加一次数学测试，共10道选择题，每题均有四个选项，答对得3分，答错或不答得0分，甲和乙都解答了所有试题，经比较，他们只有2道题的选项不同，如果甲乙的最终得分的和为54分，那么乙的所有可能的得分值组成的集合为{24，27，30}．
3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$的右焦点为F（1，0），且点P（1，$\frac{3}{2}$）在椭圆C上；
（1）求椭圆C的标准方程；
（2）过椭圆C1：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}-\frac{5}{3}}$=1上异于其顶点的任意一点Q作圆O：x2+y2=$\frac{4}{3}$的两条切线，切点分别为M、N（M、N不在坐标轴上），若直线MN在x轴，y轴上的截距分别为m、n，证明：$\frac{1}{3{m}^{2}}+\frac{1}{{n}^{2}}$为定值；
（3）若P1、P2是椭圆C2：$\frac{{x}^{2}}{{a}^{2}}+\frac{3{y}^{2}}{{b}^{2}}=1$上不同两点，P1P2⊥x轴，圆E过P1、P2，且椭圆C2上任意一点都不在圆E内，则称圆E为该椭圆的一个内切圆，试问：椭圆C2是否存在过焦点F的内切圆？若存在，求出圆心E的坐标；若不存在，请说明理由．
13．由方程|z|2-8|z|+15=0所确定的复数在复平面内对应点的轨迹是以原点为圆心，以3和5为半径的两个圆．
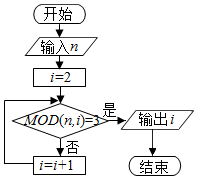20．已知MOD函数是一个求余函数，其格式为MOD（n，m），其结果为n除以m的余数，例如MOD（7，3）=1，如图是一个算法的程序框图，当输入的n值为15时，输出的结果为（　　）
A．4B．5C．6D．7
17．已知正项数列{an}满足a1=22，an+1（an+1-2n）=an（an+2n），则当$\frac{{a}_{n}}{n}$取得最小值时，n=5．
18．已知关于x的不等式-x2+x-2k＜0（k≠0）．
（1）若不等式的解集为{x|x＜-1，或x＞2}，求k的值；
（2）若不等式的解集为R，求k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网