题目内容
一元二次不等式x2-x-2＞0的解集是（ ）
| A、（∞，-1）∪（2，+∞） |
| B、（-1，2） |
| C、（-∞，-2）∪（1，+∞） |
| D、（-2，1） |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：通过因式分解，利用一元二次不等式的解法即可得出．
解答：
解：不等式x2-x-2＞0化为（x-2）（x+1）＞0，解得x＞2或x＜-1．
∴不等式x2-x-2＞0的解集是（-∞，-1）∪（2，+∞）．
故选：A．
∴不等式x2-x-2＞0的解集是（-∞，-1）∪（2，+∞）．
故选：A．
点评：本题考查了一元二次不等式的解法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知复数z1=a-i，z2=1-2i，若
是纯虚数，则实数a的值为（ ）
| z1 |
| z2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
根据图所示的算法流程图，输出的结果T为（ ）
| A、8 | B、48 | C、49 | D、50 |
一个样本容量为10的样本数据，它们组成一个公差不为0的等差数列{an}，若a8=15，且a1，a2，a5成等比数列，则此样本的平均数和中位数分别是（ ）
| A、11，10 |
| B、10，10 |
| C、11，12 |
| D、10，12 |
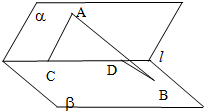如图，已知二面角α-l-β为60°，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足，且AC=2，CD=3，DB=1，则AB的长度为（ ）计算：sin225°的值为（ ）
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|