题目内容
已知f(x)=
,则不等式xf(x)+x≤2的解集为( )
|
| A、[0,1] |
| B、[0,2] |
| C、(-∞,2] |
| D、(-∞,1] |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:分类讨论,分x≥0、x<0时解答,最后求并集即可.
解答:
解:x≥0时,f(x)=1,
不等式xf(x)+x≤2可化为2x≤2
解得x≤1,∴0≤x≤1;
当x<0时,f(x)=0,
不等式xf(x)+x≤2可化为x≤2,
∴x<0.
综上可得x≤1.
故选:D
不等式xf(x)+x≤2可化为2x≤2
解得x≤1,∴0≤x≤1;
当x<0时,f(x)=0,
不等式xf(x)+x≤2可化为x≤2,
∴x<0.
综上可得x≤1.
故选:D
点评:本题考查分类讨论法解不等式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=(a2-1)x为R上的减函数,则实数a的取值范围是( )
| A、(1,2) | ||||
B、(1,
| ||||
C、(-
| ||||
| D、以上都不对 |
若不等式ax2+2x+c>0和(2x-1)(3x+1)<0有相同的解集,则不等式2x-cx2-a>0的解集是( )
| A、(-2,3) | ||||
| B、(3,+∞)∪(-∞,-2) | ||||
C、(
| ||||
D、(-
|
在△ABC中,若sin2A+sin2B=sin2C,则角C为( )
| A、钝角 | B、直角 | C、锐角 | D、60° |
一个几何体的三视图如图,则组成该组合体的简单几何体为( )


| A、圆柱与圆台 |
| B、四棱柱与四棱台 |
| C、圆柱与四棱台 |
| D、四棱柱与圆台 |
下面四个命题正确的是( )
| A、10以内的质数集合是{0,2,3,5,7} |
| B、由1,2,3组成的集合可表示为{1,2,3}或{3,1,2} |
| C、方程x2-2x+1=0的解集是{1,1} |
| D、0与{0}表示同一个集合 |
如图(1)、(2)、(3)、(4)是四个几何体的三视图,这四个几何体依次分别是( )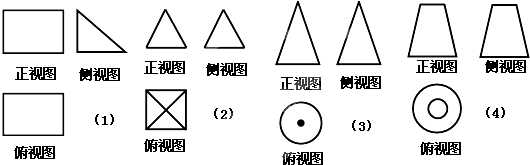

| A、三棱台、三棱柱、圆锥、圆台 |
| B、三棱台、三棱锥、圆锥、圆台 |
| C、三棱柱、四棱锥、圆锥、圆台 |
| D、三棱柱、三棱台、圆锥、圆台 |