题目内容
已知数列{bn}的前n项和为Bn,且满足 ,则b10的最小可能值为
,则b10的最小可能值为
- A.

- B.

- C.1
- D.-1
D
分析:根据数列递推式,确定数列相邻项的关系,再确定数列的首项,即可得到结论.
解答:由(bn+1)(4bn-1)=6Bn①可得:当n≥2时,(bn-1+1)(4bn-1-1)=6Bn-1②
①-②可得: -3(bn+bn-1)=0
-3(bn+bn-1)=0
∴bn+bn-1=0或
∵n=1时,(b1+1)(4b1-1)=6B1,∴b1=1或b1=-
若bn+bn-1=0,b1=1,则b10=-1;b1=- ,则b10=
,则b10=
若 ,b1=1,则b10=1+9×
,b1=1,则b10=1+9× =
=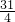 ;b1=-
;b1=- ,则b10=-
,则b10=- +9×
+9× =
=
综上,b10的最小可能值为-1
故选D.
点评:本题考查数列递推式,考查数列的通项,解题的关键是确定数列相邻项的关系.
分析:根据数列递推式,确定数列相邻项的关系,再确定数列的首项,即可得到结论.
解答:由(bn+1)(4bn-1)=6Bn①可得:当n≥2时,(bn-1+1)(4bn-1-1)=6Bn-1②
①-②可得:
 -3(bn+bn-1)=0
-3(bn+bn-1)=0∴bn+bn-1=0或

∵n=1时,(b1+1)(4b1-1)=6B1,∴b1=1或b1=-

若bn+bn-1=0,b1=1,则b10=-1;b1=-
 ,则b10=
,则b10=
若
 ,b1=1,则b10=1+9×
,b1=1,则b10=1+9× =
=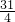 ;b1=-
;b1=- ,则b10=-
,则b10=- +9×
+9× =
=
综上,b10的最小可能值为-1
故选D.
点评:本题考查数列递推式,考查数列的通项,解题的关键是确定数列相邻项的关系.

练习册系列答案
相关题目