题目内容
3.已知函数$f(x)=x-\frac{a}{x}$,g(x)=2ln(x+m).(1)当m=0,存在x0∈[$\frac{1}{e}$,e](e为自然对数的底数),使$f({x_0})≥\frac{{g({x_0})}}{x_0}$,求实数a的取值范围;
(2)当a=m=1时,设H(x)=xf(x)+g(x),在H(x)的图象上是否存在不同的两点A(x1,y1),B(x2,y2)(x1>x2>-1),使得H(x1)-H(x2)=$H'(\frac{{{x_1}+{x_2}}}{2})•({x_1}-{x_2})$?请说明理由.
分析 (1)x0f(x0)≥g(x0)可化为$a≤{x_0}^2-2ln{x_0}$,
构造h(x)=x2-2lnx,求出其值域即可.
(2)$\frac{{H({x_1})-H({x_2})}}{{{x_1}-{x_2}}}=\frac{2}{{{x_1}-{x_2}}}ln\frac{{{x_1}+1}}{{{x_2}+1}}+({x_1}+{x_2})$;$H'(\frac{{{x_1}+{x_2}}}{2})=\frac{4}{{{x_1}+{x_2}+2}}+({x_1}+{x_2})$;
故可化为$\frac{2}{{{x_1}-{x_2}}}ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{4}{{{x_1}+{x_2}+2}}$,即$ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{{2({x_1}-{x_2})}}{{{x_1}+{x_2}+2}}$
又即$ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{{2[({x_1}+1)-({x_2}+1)]}}{{({x_1}+1)+({x_2}+1)}}=\frac{{2[\frac{{{x_1}+1}}{{{x_2}+1}}-1]}}{{\frac{{{x_1}+1}}{{{x_2}+1}}+1}}$①,
令$\frac{{{x_1}+1}}{{{x_2}+1}}=t(t>1)$,①式可化为$lnt=\frac{2(t-1)}{t+1}$
令$u(t)=lnt-\frac{2(t-1)}{t+1}$,$u'(t)=\frac{{{{(t-1)}^2}}}{{t{{(t+1)}^2}}}>0$,只需考查u(t)的值域即可.
解答 解:(1)x0f(x0)≥g(x0)可化为$a≤{x_0}^2-2ln{x_0}$,
令h(x)=x2-2lnx,则$h'(x)=\frac{2(x+1)(x-1)}{x}(x>0)$
∴当x∈$[\frac{1}{e},1)$时,h'(x)<0;当x∈(1,e]时,h'(x)>0;
又∵$h(\frac{1}{e})=\frac{1}{e^2}+2<h(e)={e^2}-2$,∴$h{(x)_{max}}={e^2}-2$,则a≤e2-2.…5分
(2)H(x)=x2+2ln(x+1)-1,$H'(x)=\frac{2}{x+1}+2x$;
$\frac{{H({x_1})-H({x_2})}}{{{x_1}-{x_2}}}=\frac{2}{{{x_1}-{x_2}}}ln\frac{{{x_1}+1}}{{{x_2}+1}}+({x_1}+{x_2})$;
$H'(\frac{{{x_1}+{x_2}}}{2})=\frac{4}{{{x_1}+{x_2}+2}}+({x_1}+{x_2})$;
故可化为$\frac{2}{{{x_1}-{x_2}}}ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{4}{{{x_1}+{x_2}+2}}$,即$ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{{2({x_1}-{x_2})}}{{{x_1}+{x_2}+2}}$…7分
又即$ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{{2[({x_1}+1)-({x_2}+1)]}}{{({x_1}+1)+({x_2}+1)}}=\frac{{2[\frac{{{x_1}+1}}{{{x_2}+1}}-1]}}{{\frac{{{x_1}+1}}{{{x_2}+1}}+1}}$①,
令$\frac{{{x_1}+1}}{{{x_2}+1}}=t(t>1)$,①式可化为$lnt=\frac{2(t-1)}{t+1}$,…9分
令$u(t)=lnt-\frac{2(t-1)}{t+1}$,$u'(t)=\frac{{{{(t-1)}^2}}}{{t{{(t+1)}^2}}}>0$,∴u(t)在(1,+∞)上递增…11分
∴u(t)≥u(1)=0;∴u(t)无零点,故A、B两点不存在.…12分.
点评 本题考查导数的几何意义、运算及应用,涉及分离变量、构造函数、换元法以及转化思想,属于中档题.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案| A. | 0 | B. | a | C. | 1 | D. | 1-a |
| A. | 2$α+β=\frac{π}{2}$ | B. | 3$α+β=\frac{π}{2}$ | C. | 2$α-β=\frac{π}{2}$ | D. | 3$α-β=\frac{π}{2}$ |
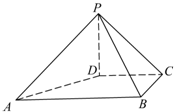 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.(1)求PB和平面PAD所成角的正弦值.
(2)求面PAD和面PBC所成二面角的大小.
| A. | (-4,1) | B. | (-1,4) | C. | (-∞,-$\frac{3}{2}$) | D. | (-∞,$\frac{3}{2}$) |