题目内容
15.函数f(x)=x3+x2单调递减区间是[-$\frac{2}{3}$,0].分析 根据f(x)的导函数建立不等关系,可得f'(0)≤0,建立不等量关系,求出单调递减区间即可.
解答 解:∵f′(x)=3x2+2x,
∴3x2+2x≤0,
解得-$\frac{2}{3}$≤x≤0,
∴函数f(x)=x3+x2单调递减区间是[-$\frac{2}{3}$,0],
故答案为:[-$\frac{2}{3}$,0].
点评 本小题主要考查运用导数研究函数的单调性等基础知识,考查分析和解决问题的能力.

练习册系列答案
相关题目
4.设函数f(x)=ex-e-x-2x,下列结论正确的是( )
| A. | f(2x)min=f(0) | B. | f(2x)max=f(0) | ||
| C. | f(2x)在(-∞,+∞)上递减,无极值 | D. | f(2x)在(-∞,+∞)上递增,无极值 |
5.在四面体P-ABC的四个面中,是直角三角形的面至多有( )个.
| A. | 0个 | B. | 1个 | C. | 3个 | D. | 4个 |
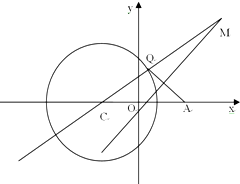 如图,已知圆$C:{(x+\sqrt{3})^2}+{y^2}=8,A(\sqrt{3},0)$,Q是圆上一动点,AQ的垂直平分线交直线CQ于点M,设点M的轨迹为E.
如图,已知圆$C:{(x+\sqrt{3})^2}+{y^2}=8,A(\sqrt{3},0)$,Q是圆上一动点,AQ的垂直平分线交直线CQ于点M,设点M的轨迹为E.