题目内容
定义在R上的奇函数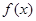 有最小正周期4,且
有最小正周期4,且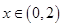 时,
时,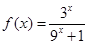 。
。
(1)求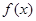 在
在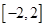 上的解析式;
上的解析式;
(2)判断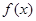 在
在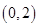 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当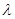 为何值时,关于方程
为何值时,关于方程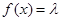 在
在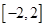 上有实数解?
上有实数解?
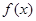 有最小正周期4,且
有最小正周期4,且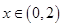 时,
时,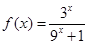 。
。(1)求
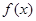 在
在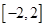 上的解析式;
上的解析式;(2)判断
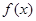 在
在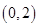 上的单调性,并给予证明;
上的单调性,并给予证明;(3)当
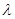 为何值时,关于方程
为何值时,关于方程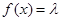 在
在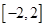 上有实数解?
上有实数解?(1) (2)
(2)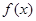 在(0,2)上单调递减;(3)
在(0,2)上单调递减;(3)
 (2)
(2)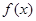 在(0,2)上单调递减;(3)
在(0,2)上单调递减;(3)
试题分析:(1)当
 时,
时, ,利用
,利用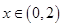 时,
时,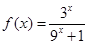 ,可得
,可得
 ,当
,当 时,由
时,由 ,可得
,可得 ,又
,又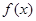 的最小正周期4,可得
的最小正周期4,可得 ,由此可求
,由此可求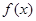 在[-2,2]上的解析式;(2)直接利用函数单调性的定义去求;(3)利用
在[-2,2]上的解析式;(2)直接利用函数单调性的定义去求;(3)利用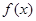 在(0,2)上单调递减和
在(0,2)上单调递减和 为奇函数,分别求出
为奇函数,分别求出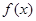 在
在 、
、 、
、 上的范围,从而得出
上的范围,从而得出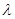 的取值范围.
的取值范围.试题解析:(1)

 1分
1分当
 时,
时, ,故
,故
 3分
3分 4分
4分(2)任取
 ,
, 6分
6分因为
 故
故 ,
, ,
, >0
>0 故
故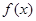 在(0,2)上单调递减。 8分
在(0,2)上单调递减。 8分(3)由(2)知:
 时,
时,

又
 为奇函数,
为奇函数, 时,
时,

 时,
时,
综上:
 12分
12分
练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 ,
, ,则函数
,则函数 的值域为( )
的值域为( )



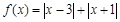 .
.
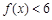 成立的
成立的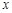 的取值范围;
的取值范围;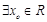 ,
,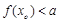 ,求实数
,求实数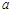 的取值范围.
的取值范围.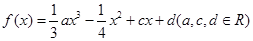 满足
满足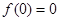 ,
,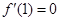 且
且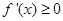 在
在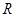 上恒成立.
上恒成立.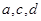 的值;
的值;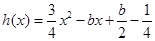 ,解不等式
,解不等式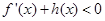 ;
;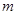 ,使函数
,使函数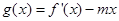 在区间
在区间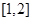 上有最小值
上有最小值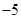 ?若存在,请求出实数
?若存在,请求出实数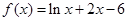 的零点位于( )
的零点位于( )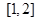
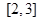
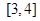
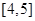
 -lnx,则y=f(x)( )
-lnx,则y=f(x)( ) ,1),(1,e)内均有零点
,1),(1,e)内均有零点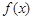 的定义域为D,如果
的定义域为D,如果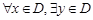 ,使
,使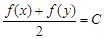 (C为常数
(C为常数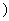 成立,则称函数
成立,则称函数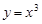 ;②
;②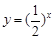 ;③
;③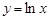 ;④
;④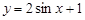 ,则满足在其定义域上均值为1的函数的个数是( )
,则满足在其定义域上均值为1的函数的个数是( )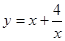
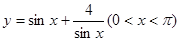
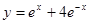
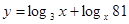
 ,则
,则