题目内容
设函数f(x)= -lnx,则y=f(x)( )
-lnx,则y=f(x)( )
 -lnx,则y=f(x)( )
-lnx,则y=f(x)( )A.在区间( ,1),(1,e)内均有零点 ,1),(1,e)内均有零点 |
B.在区间( ,1),(1,e)内均无零点 ,1),(1,e)内均无零点 |
C.在区间( ,1)内有零点,在区间(1,e)内无零点 ,1)内有零点,在区间(1,e)内无零点 |
D.在区间( ,1)内无零点,在区间(1,e)内有零点 ,1)内无零点,在区间(1,e)内有零点 |
D
试题分析:
 ,
, ,所以
,所以 在区间(
在区间( ,1)内无零点,在区间(1,e)内有零点,选D.
,1)内无零点,在区间(1,e)内有零点,选D.
练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
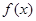 有最小正周期4,且
有最小正周期4,且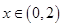 时,
时,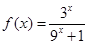 。
。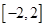 上的解析式;
上的解析式;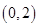 上的单调性,并给予证明;
上的单调性,并给予证明;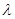 为何值时,关于方程
为何值时,关于方程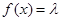 在
在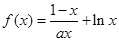
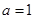 时,求
时,求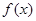 在
在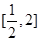 上的最小值;
上的最小值;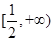 上为增函数,求正实数
上为增函数,求正实数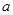 的取值范围;
的取值范围;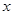 的方程
的方程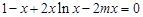 在区间
在区间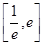 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数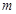 的取值范围.
的取值范围. 的一个零点在区间
的一个零点在区间 内,则实数
内,则实数 的取值范围是 .
的取值范围是 .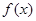 ,若
,若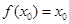 ,则称
,则称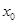 为函数
为函数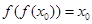 ,则称
,则称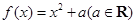 的“稳定点”恰是它的“不动点”,那么实数
的“稳定点”恰是它的“不动点”,那么实数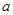 的取值范围是( )
的取值范围是( )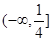
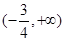
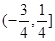
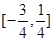
 (k∈R),若函数
(k∈R),若函数 有三个零点,则实数k的取值范围是( )
有三个零点,则实数k的取值范围是( )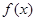 的定义域为
的定义域为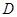 ,若存在非零实数
,若存在非零实数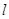 使得对于任意
使得对于任意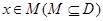 ,有
,有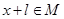 ,且
,且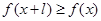 ,则称
,则称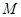 上的
上的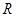 的函数
的函数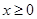 时,
时,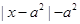 ,且
,且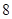 高调函数,那么实数
高调函数,那么实数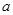 的取值范围是
的取值范围是  ,则
,则 ( )
( ) ,其中
,其中 ,
, ,已知对所有的有序正整数对
,已知对所有的有序正整数对 满足下述条件:①
满足下述条件:① ,②若
,②若 ,
, ;③
;③ ,则
,则 .
.