题目内容
2.已知等腰三角形ABC中,|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|=5,|$\overrightarrow{BC}$|=6,点D为底边上一动点,$\overrightarrow{DA}$•$\overrightarrow{DC}$取最小值时,则|$\overrightarrow{DC}$|=$\frac{3}{2}$.分析 建立如图所示的直角坐标系,O(0,0),A(0,4),C(3,0),D(x,0),(-3≤x≤3).可得:$\overrightarrow{DA}$•$\overrightarrow{DC}$=(-x,4)•(3-x,0)=-x(3-x),利用基本不等式的性质即可得出最小值.
解答 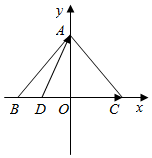 解:建立如图所示的直角坐标系
解:建立如图所示的直角坐标系
O(0,0),A(0,4),C(3,0),D(x,0),(-3≤x≤3).
∴$\overrightarrow{DA}$•$\overrightarrow{DC}$=(-x,4)•(3-x,0)=-x(3-x)≥$-(\frac{x+3-x}{2})^{2}$=-$\frac{9}{4}$,当且仅当x=$\frac{3}{2}$时取等号,
∴$\overrightarrow{DC}$=$(\frac{3}{2},0)$.
则|$\overrightarrow{DC}$|=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了向量数量积运算性质、基本不等式的性质、模的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知点$Q({-2\sqrt{2},0})$及抛物线x2=-4y上一动点P(x,y),则|y|+|PQ|的最小值是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
11.如果一个数列{an}满足an+an+1=H(H为常数,n∈N*),则称数列{an}为等和数列,H为公和,Sn是其前n项的和,已知等和数列{an}中,a1=1,H=-3,则S2011等于( )
| A. | -3016 | B. | -3015 | C. | -3014 | D. | -3013 |