题目内容
计算:-1+3、-1+3-5、-1+3-5+7、…,根据计算结果找规律填空:-1+3-5+7+…+(-1)n(2n-1)= .
考点:归纳推理
专题:规律型
分析:由已知中的前若干个式子,分析出结果与n的关系,找出规律后,可得答案.
解答:
解:∵-1+3=2=(-1)2×2;
-1+3-5=-3=(-1)3×3;
-1+3-5+7=4=(-1)4×4;
…,
由此归纳可得:-1+3-5+7+…+(-1)n(2n-1)=(-1)nn;
故答案为:(-1)nn
-1+3-5=-3=(-1)3×3;
-1+3-5+7=4=(-1)4×4;
…,
由此归纳可得:-1+3-5+7+…+(-1)n(2n-1)=(-1)nn;
故答案为:(-1)nn
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
中国古代数学著作《九章算法》中的“更相减损术”可用来求两个正整数的最大公约数.现应用此法求168与93的最大公约数:记(168,93)为初始状态,则第一步可得(75,93),第二步得到(75,18),….以上解法中,不会出现的状态是( )
| A、(57,18) |
| B、(3,18) |
| C、(6,9) |
| D、(3,3) |
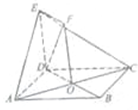 如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=
如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=