题目内容
4.函数y=a0+a1x+a2x2+…+anxn(a0,a1,a2,…,an∈R)的导数是y′=a1+2a2x+…+nanxn-1(a1,a2,…,an∈R).分析 根据导数的公式进行求导即可.
解答 解:∵y=a0+a1x+a2x2+…+anxn(a0,a1,a2,…,an∈R),
∴函数的导数y′=a1+2a2x+…+nanxn-1(a1,a2,…,an∈R),
故答案为:y′=a1+2a2x+…+nanxn-1(a1,a2,…,an∈R)
点评 本题主要考查函数的导数的计算,要求熟练掌握掌握常见函数的导数公式,比较基础.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
14.某几何体的三视图如图,则该几何体的表面积为( )
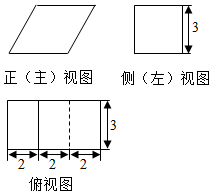

| A. | 48+6$\sqrt{13}$ | B. | 78 | C. | 24+6$\sqrt{13}$ | D. | 68 |
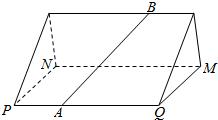 如图,某人沿山坡PQB的直行道AB向上行走,直行道AB与坡脚(直)线PQ成60°角,山坡与地平面所成二面角B-PQ-M的大小为30°.
如图,某人沿山坡PQB的直行道AB向上行走,直行道AB与坡脚(直)线PQ成60°角,山坡与地平面所成二面角B-PQ-M的大小为30°.