题目内容
已知椭圆C过点A(1,
),两焦点为F1(-
,0)、F2(
,0),O是坐标原点,不经过原点的直线l:y=kx+m与该椭圆交于两个不同点P、Q,且直线OP、PQ、OQ的斜率依次成等比数列.
(1)求椭圆C的方程;
(2)求直线l的斜率k;
(3)求△OPQ面积的范围.
| ||
| 2 |
| 3 |
| 3 |
(1)求椭圆C的方程;
(2)求直线l的斜率k;
(3)求△OPQ面积的范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得c=
,设椭圆方程为
+
=1,则
+
=1,由此能求出椭圆C的方程.
(2)由
,得:(1+4k2)x2+8kmx+4(m2-1)=0,由此利用根的判别式、韦达定理、等比数列结合已知条件能求出k.
(3)直线OQ的斜率存在且不为0,及△>0,得0<m2<2,且m≠1,求出点O到直线l的距离,由此能求出S△OPQ的取值范围.
| 3 |
| x2 |
| b2+3 |
| y2 |
| b2 |
| 1 |
| b2+3 |
| 3 |
| 4b2 |
(2)由
|
(3)直线OQ的斜率存在且不为0,及△>0,得0<m2<2,且m≠1,求出点O到直线l的距离,由此能求出S△OPQ的取值范围.
解答:
解:(1)∵椭圆C过点A(1,
),两焦点为F1(-
,0)、F2(
,0),
∴c=
,设椭圆方程为
+
=1…(2分)
则
+
=1,
解得b2=1,
∴椭圆C的方程为
+y2=1.…(4分)
(2)由
,消去y得:(1+4k2)x2+8kmx+4(m2-1)=0…(6分)
则△=64k2m2-16(1+4k2)(m2-1)
=16(4k2-m2+1)>0,
x1+x2=-
,x1x2=
,
故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2…(8分)
∵直线OP、PQ、OQ的斜率依次成等比数列,
∴
•
=
=k2⇒km(x1+x2)+m2=0⇒-
+m2=0,
由于m≠0,故k2=
⇒k=±
,
∴直线l的斜率k为±
.…(10分)
(3)∵直线OQ的斜率存在且不为0,及△>0
∴0<m2<2,且m≠1.…(12分)
设d为点O到直线l的距离,
则S△OPQ=
d|PQ|═
•
|x1-x2|
=
|m|
=
…(14分)
则S△OPQ<
=1,
∴S△OPQ的取值范围为(0,1).…(16分)
| ||
| 2 |
| 3 |
| 3 |
∴c=
| 3 |
| x2 |
| b2+3 |
| y2 |
| b2 |
则
| 1 |
| b2+3 |
| 3 |
| 4b2 |
解得b2=1,
∴椭圆C的方程为
| x2 |
| 4 |
(2)由
|
则△=64k2m2-16(1+4k2)(m2-1)
=16(4k2-m2+1)>0,
x1+x2=-
| 8km |
| 1+4k2 |
| 4(m2-1) |
| 1+4k2 |
故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2…(8分)
∵直线OP、PQ、OQ的斜率依次成等比数列,
∴
| y1 |
| x1 |
| y2 |
| x2 |
| k2x1x2+km(x1+x2)+m2 |
| x1x2 |
| 8k2m2 |
| 1+4k2 |
由于m≠0,故k2=
| 1 |
| 4 |
| 1 |
| 2 |
∴直线l的斜率k为±
| 1 |
| 2 |
(3)∵直线OQ的斜率存在且不为0,及△>0
∴0<m2<2,且m≠1.…(12分)
设d为点O到直线l的距离,
则S△OPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| |m| | ||
|
| 1+k2 |
=
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
| m2(2-m2) |
则S△OPQ<
| m2+2-m2 |
| 2 |
∴S△OPQ的取值范围为(0,1).…(16分)
点评:本题考查椭圆方程的求法,考查直线的斜率的求法,考查三角形面积的取值范围的求法,解题时要认真审题,注意弦长公式的合理运用.

练习册系列答案
相关题目
 人民日报3月14日报道,中国人民银行已下发通知,要求暂停二维码(条码)支付,虚拟信用卡等支付业务和产品.前不久,某调研机构调研了在校大学生网上购物的情况,随机调查了16位在校大学生的网购比例,结果如茎叶图所示(图中茎7叶3表示73%,其余相同):
人民日报3月14日报道,中国人民银行已下发通知,要求暂停二维码(条码)支付,虚拟信用卡等支付业务和产品.前不久,某调研机构调研了在校大学生网上购物的情况,随机调查了16位在校大学生的网购比例,结果如茎叶图所示(图中茎7叶3表示73%,其余相同): 在四面体ABCD中,已知AC⊥BD,∠BAC=∠CAD=45°,∠BAD=60°,求证:平面ABC⊥平面ACD.
在四面体ABCD中,已知AC⊥BD,∠BAC=∠CAD=45°,∠BAD=60°,求证:平面ABC⊥平面ACD.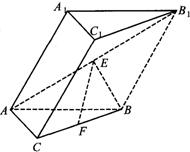 如图,在斜三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.