题目内容
6.已知,点P(x,y)的坐标满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≤6}\\{y-1≥0}\end{array}\right.$设A(2,0),则|$\overrightarrow{OP}$|cos∠AOP(O为坐标原点)的最大值为1.分析 先根据约束条件画出可行域,利用向量的数量积得|$\overrightarrow{OP}$|•cos∠AOP=x,再利用z的几何意义求最值.
解答 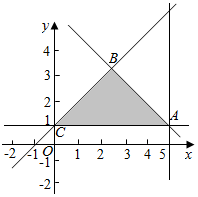 解:在平面直角坐标系中画出不等式组所表示的可行域(如图),
解:在平面直角坐标系中画出不等式组所表示的可行域(如图),
由于|$\overrightarrow{OP}$|•cos∠AOP=$\frac{|\overrightarrow{OP}||\overrightarrow{OA}|cos∠AOP}{|\overrightarrow{OA}|}$=$\frac{\overrightarrow{OP}•\overrightarrow{OA}}{|\overrightarrow{OA}|}$=$\frac{(2,0)•(x,y)}{2}$═$\frac{2x}{2}=x$,
令z=x,
平移直线x=z,
由图形可知,当直线经过可行域中的点A时,x最大,
由$\left\{\begin{array}{l}{y=1}\\{x+y=6}\end{array}\right.$,解得x=5,y=1,
所以|$\overrightarrow{OP}$|•cos∠AOP的最大值为1.
故答案为:1.
点评 本题主要考查了向量的数量积、简单的线性规划,以及利用几何意义求最值.巧妙识别目标函数的几何意义是我们研究规划问题的基础.

练习册系列答案
相关题目