题目内容

18．已知正四棱锥S-ABCD底面边长与高都是2，K是SC的中点，T是SB中点，求证：KT∥平面SAD．

分析 由已知得KT∥BC，BC∥AD，从而KT∥AD，由此能证明KT∥平面SAD．

解答 证明：∵正四棱锥S-ABCD，底面边长与高都是2，K是SC的中点，T是SB的中点，
∴KT∥BC，BC∥AD，
∴KT∥AD，
∵KT?平面SAD，AD?平面SAD，
∴KT∥平面SAD．

点评 本题考查直线与平面平行的证明．若平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行．

练习册系列答案
相关题目
9．已知三角形ABC的面积为1，tanB=$\frac{1}{2}$，tanC=-2，求三角形ABC的各边长及外接圆的面积．
10．判断下列各题中的向量$\overrightarrow{a}$与$\overrightarrow{b}$是否共线：
（1）$\overrightarrow{a}$=-2$\overrightarrow{e}$，$\overrightarrow{b}$=2$\overrightarrow{e}$
（2）$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=-2$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$．
7．已知{an}是等差数列，且a1=1，a1+a2+a3=6，令bn=an•2n，求{bn}的前n项的和Tn．

定义域为的连续可导函数，若满足以下两个条件：

①的导函数没有零点，②对，都有.

则关于方程有（ ）个解.

A．2 B．1 C．0 D．以上答案均不正确
3．执行如图所示的程序框图，则输出S的值是（　　）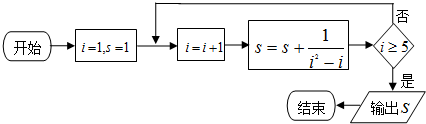
A．$\frac{4}{5}$B．$\frac{9}{5}$C．$\frac{5}{6}$D．$\frac{11}{6}$
10．极坐标系内，O为极点，设点A（3，$\frac{π}{6}$），B（4，$\frac{2π}{3}$），则三角形AOB的面积为6．
7．设椭圆中心在坐标原点，A（2，0），B（0，1）是它的两个顶点，直线y=kx（k＞0）与AB相交于点D，与椭圆相交于E，F两点，若$\overrightarrow{ED}$=6$\overrightarrow{DF}$，则所有k的值为$\frac{2}{3}$或$\frac{3}{8}$．
6．若程序框图如图所示，则该程序框图表示的算法输出的i是10．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网