题目内容
18.设x1,x2,…,x10为1,2,…,10的一个排列,则满足对任意正整数m,n,且1≤m<n≤10,都有xm+m≤xn+n成立的不同排列的个数为( )| A. | 512 | B. | 256 | C. | 255 | D. | 64 |
分析 利用归纳推理求出n的最大值分别为2,3,4时的排列个数,然后推出本题的结果.
解答 解:如果n=2时,满足题意的排列个数是2,即1,2或2,1;即21.
如果n的最大值为3,则排列个数为4;分别为:1,2,3; 2,1,3;1,3,2;3,2,1;4个.即22.
如果n的最大值为4,则满足题意的排列个数为8;分别为:1,2,3,4;2,1,3,4;2,1,4,3;1,3,2,4;1,2,4,3,;3,1,2,4;1,4,3,2;4,3,2,1;共8个,即23.
如果n的最大值为5,则满足题意的排列个数为16;分别为:1,2,3,4,5;2,1,3,4,5;2,1,4,3,5;2,1,3,5,4;2,1,5,4,3;1,2,4,3,5;1,2,3,5,4;1,2,5,4,3;1,3,2,4,5;1,3,2,5,4;1,4,3,2,5;1,5,4,3,2;3,2,1,4,5;3,2,1,5,4;4,3,2,1,5;5,4,3,2,1;即24.
…
所以:设x1,x2,…,x10为1,2,…,10的一个排列,则满足对任意正整数m,n,且1≤m<n≤10,都有xm+m≤xn+n成立的不同排列的个数为:29=512.
故答案为:512.
点评 本题考查排列组合的数据应用,归纳推理的应用,解题的关键是:1≤m<n≤10,都有xm+m≤xn+n成立的理解,本题是难题.

练习册系列答案
相关题目
13.已知tanα=-$\frac{3}{4}$,且α∈(0,π),则cosα=( )
| A. | $\frac{4}{5}$ | B. | $\frac{1}{2}$ | C. | -$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
10.已知定义在R上的可导函数f(x)的导函数为f'(x),满足f'(x)<f(x),且f(x+3)为偶函数,f(6)=1,则不等式f(x)>ex的解集为( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
7.设集合A={x|x≤0或x≥2},B={x|x<1},则集合A∩B=( )
| A. | (-∞,0) | B. | (-∞,0] | C. | [2,+∞) | D. | (2,+∞) |
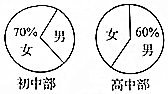 某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为137.
某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为137.