题目内容
5.等差数列{an}的前n项和为Sn,已知a2=7,a3为整数,且Sn的最大值为S5.(1)求{an}的通项公式;
(2)设bn=$\frac{{a}_{n}}{{2}^{n}}$,求数列{bn}的前n项和Tn.
分析 (1)由题意列式求出公差,进一步求出首项,代入等差数列的通项公式得答案;
(2)把{an}的通项公式代入bn=$\frac{{a}_{n}}{{2}^{n}}$,然后利用错位相减法求数列{bn}的前n项和Tn.
解答 解:(1)∵等差数列{an}的前n项和Sn的最大值为S5.
∴a5≥0,则d=$\frac{{a}_{5}-{a}_{2}}{3}$=$\frac{{a}_{5}-7}{3}$$≥-\frac{7}{3}$,
a6≤0,则d=$\frac{{a}_{6}-{a}_{2}}{4}=\frac{{a}_{6}-{a}_{2}}{4}≤-\frac{7}{4}$,
∵a3=a2+d=7+d为整数,∴d=-2.
则a1=a2-d=7-(-2)=9,
∴an=9-2(n-1)=11-2n;
(2)bn=$\frac{{a}_{n}}{{2}^{n}}$=$\frac{11-2n}{{2}^{n}}$,
则${T}_{n}=9•\frac{1}{2}+7•\frac{1}{{2}^{2}}+…+$$\frac{13-2n}{{2}^{n-1}}+\frac{11-2n}{{2}^{n}}$,
$-\frac{1}{2}{T}_{n}=9•\frac{1}{{2}^{2}}+7•\frac{1}{{2}^{3}}+…+\frac{13-2n}{{2}^{n}}+\frac{11-2n}{{2}^{n+1}}$,
两式作差得:$\frac{3}{2}{T}_{n}=\frac{9}{2}-2(\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}})-\frac{11-2n}{{2}^{n+1}}$=$\frac{9}{2}-2×\frac{\frac{1}{4}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}-\frac{11-2n}{{2}^{n+1}}$
=$\frac{9}{2}-(1-\frac{1}{{2}^{n-1}})-\frac{11-2n}{{2}^{n+1}}$,
∴${T}_{n}=\frac{7}{3}+\frac{1}{3}•\frac{2n-7}{{2}^{n}}$.
点评 本题考查数列递推式,考查了错位相减法求数列的前n项和,是中档题.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案| A. | 最大值为16 | B. | 是定值24 | C. | 最小值为4 | D. | 是定值4 |
| A. | (-∞,0) | B. | (-∞,0] | C. | [2,+∞) | D. | (2,+∞) |
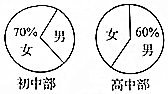 某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为137.
某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为137.