题目内容
已知函数f（x）=2x3-ax2+1在区间[1，+∞）上为单调增函数，求a的取值范围．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出函数的导数，由题意得不等式6x2-2ax≥0，得a≤3x对任意x∈[1，+∞）恒成立，设h（x）=3x，x∈[1，+∞），则a≤h（x）min，h（x）min=3，从而求出a的值．
解答：
解：f′（x）=6x2-2ax，
∵f（x）在区间[1，+∞）上单调递增，
∴f′x）≥0对任意x∈[1，+∞）恒成立，
∴6x2-2ax≥0，
∴a≤3x对任意x∈[1，+∞）恒成立，
设h（x）=3x，x∈[1，+∞），
则a≤h（x）min
∵h（x）min=3，
∴a≤3．
∵f（x）在区间[1，+∞）上单调递增，
∴f′x）≥0对任意x∈[1，+∞）恒成立，
∴6x2-2ax≥0，
∴a≤3x对任意x∈[1，+∞）恒成立，
设h（x）=3x，x∈[1，+∞），
则a≤h（x）min
∵h（x）min=3，
∴a≤3．
点评：本题考察了函数的单调性，导数的应用，求参数的范围，是一道基础题．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
已知某程序框图如图所示，则执行该程序后输出的结果是（ ）
| A、-1 | ||
B、
| ||
| C、2 | ||
| D、1 |
经过两直线l1：2x-3y+2=0与l2：3x-4y-2=0的交点，且平行于直线4x-2y+7=0的直线方程是（ ）
| A、x-2y+9=0 |
| B、4x-2y+9=0 |
| C、2x-y-18=0 |
| D、x+2y+18=0 |
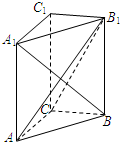如图，在直三棱柱ABC-A1B1C1中，已知CA=CB=1，AA1=2，∠BCA=90°．