题目内容
求导函数：y=ln
．
|
考点：导数的运算
专题：导数的概念及应用
分析：根据复合函数的求导法则求导即可．
解答：
解：令
=t，
∴t′=
•(
)-
•(
)′=
•(
)-
•
设y′=
•t′=
•
•(
)-
•
=
|
∴t′=
| 1 |
| 2 |
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
| 4x |
| (1-x2)2 |
设y′=
| 1 |
| t |
| 1 | ||||
|
| 1 |
| 2 |
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
| 4x |
| (1-x2)2 |
| 2x |
| 1-x4 |
点评：本题考查了复合函数的求导法则，培养了学生的计算能力，属于基础题
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
下列集合中，不同于另外三个集合的是（ ）
| A、{3} |
| B、M={y∈R|（y-3）2=0} |
| C、M={x=3} |
| D、M={x|x-3=0} |
如图，在空间四边形ABCD中，AB=BC，CD=DA，E、F、G分别是CD、DA、AC的中点，则（ ）
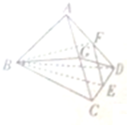
| A、平面BEF⊥平面BGD |
| B、平面ABC⊥平面ACD |
| C、CD⊥平面BEF |
| D、AB⊥平面BGD |