题目内容
设命题p：函数y=ax-1（a＞0且a≠1）过定点（1，0）；命题q：函数y=2x2-3x+1的值域是[-
，+∞）．则下列判断正确的是（ ）
| 1 |
| 8 |
| A、p为真 | B、￢q为真 |
| C、p∧q为真 | D、p∨q为真 |
考点：复合命题的真假
专题：函数的性质及应用
分析：先判定命题p，q的真假，再利用“或”“且”“非”命题的真假判断即可．
解答：
解：命题p：函数y=ax-1（a＞0且a≠1）过定点（1，1），因此命题P是假命题；
命题q：函数y=2x2-3x+1=2(x-
)2-
≥-
，
∴函数的值域是[-
，+∞），因此命题q是真命题．
∴p∨q是真命题．
故选：D．
命题q：函数y=2x2-3x+1=2(x-
| 3 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
∴函数的值域是[-
| 1 |
| 8 |
∴p∨q是真命题．
故选：D．
点评：本题考查了复合命题真假的判断、函数的性质，属于基础题．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
一个几何体的正视图和侧视图都是矩形，俯视图是一个圆（如图所示），该几何体的体积为（ ）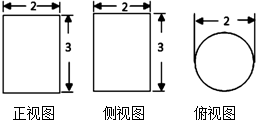
| A、π | B、2π | C、3π | D、4π |
复数
的实部和模分别为（ ）
| 2 |
| 1-i |
| A、1，2 | ||
| B、i，2 | ||
C、1，
| ||
D、i，
|
已知集合A={x|x2-2x≤0}，B={x|y=log2（x-1）}，则A∩B=（ ）
| A、{x|1≤x＜2} |
| B、{x|1＜x＜2} |
| C、{x|1＜x≤2} |
| D、{x|1≤x≤2} |
设函数f（x）=x2+alnx，则（ ）
A、f（x）的单调递增区间为[
| ||||
| B、f（x）＞0对任意x∈（0，+∞）恒成立 | ||||
| C、f（x）的图象与x轴至多一个交点 | ||||
| D、若f（x）有极值点x1，则f（x1）≤1 |
设集合A={x|y=ln（x+1）}，B={-2，-1，0，1}，则（∁RA）∩B=（ ）
| A、{-2} |
| B、{-2，-1} |
| C、{-2，-1，0} |
| D、{-2，-1，0，1} |
设l、m两条不同的直线，α是一个平面，则下列命题不正确的是（ ）
| A、若l⊥α，m?α，则l⊥m |
| B、若l⊥α，l∥m，则m⊥α |
| C、若l⊥α，则m⊥α，则l∥m |
| D、若l∥α，m∥α，则l∥m |