题目内容
(
温州十校模拟)如下图,四棱锥P—ABCD中,PA⊥ABCD,四边形ABCD是矩形.E、F分别是AB、PD的中点.若PA=AD=3,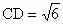 .
.
(1)
求证:AF∥平面PCE;(2)
求点F到平面PCE的距离;(3)
求直线FC与平面PCE所成角的大小.
答案:略
解析:
解析:
|
解析: (1)取PC的中点G,连结EG,FG,
又由 F为PD的中点,则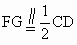 . .
又由已知有 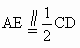 ,∴FG ,∴FG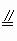 AE. AE.
∴四边形 AEGF是平行四边形.∴ AE∥EG.又 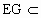 平面PCE. 平面PCE.
∴ AF∥平面PCE. (5分)(2) ∵PA⊥平面ABCD,∴平面 PAD⊥ABCD.由 ABCD是矩形有CD⊥AD.∴ CD⊥平面PAD.∴AF⊥CD.又 PA=AD=3,F是PD的中点,∴AF⊥PD.∵ PD∩CD=D,∵AF⊥平面PCD.由 EG∥AF,∴EG⊥平面PCD.∴在平面 PCD内,过F作FH⊥PC于H,由于平面 PCD∩平面PCE=PC,则FH的长就是点F到平面PCE的距离.(8 分)由已知可得
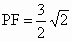 , ,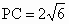 . .
由于 CD⊥平面PAD,∴∠CPD=30°.∴ ∴点 F到平面PCE的距离为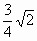 . (10分) . (10分)
(3) 由(2)知∠FCH为直线FC与平面PCE所成的角.在 Rt△CDF中,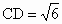 , ,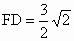 , ,
∴ ∴ ∴直线 FC与平面PCE所成角的大小为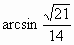 . (14分) . (14分) |

练习册系列答案
相关题目


 .
. .
. .
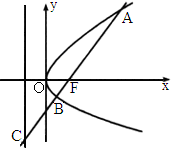
.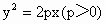 的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
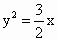
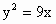
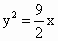
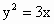
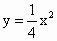 的焦点,离心率等于
的焦点,离心率等于 .
.
 ,求证
,求证 为定值.
为定值. β,则α⊥β
β,则α⊥β
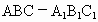 中,∠ACB=90°,
中,∠ACB=90°,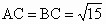 ,
,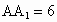 ,E、F分别为
,E、F分别为 与
与 的中点.
的中点.
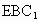 与平面ABC所成的锐二面角的大小.
与平面ABC所成的锐二面角的大小.
