题目内容
定义:若对任意x1、x2∈(a,b)恒有f(
)≤
成立,则称函数f(x)在(a,b)上为凹函数.已知凹函数具有如下性质:对任意的xi∈(a,b)(i=1,2,…,n),必有f(
)≤
成立,其中等号当且仅当x1=x2=…=xn时成立.
(1)试判断y=x2是否为R上的凹函数,并说明理由;
(2)若x、y、z∈R,且x+y+2z=8,试求x2+y2+2z2的最小值并指出取得最小值时x、y、z的值.
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2+…+xn |
| n |
| f(x1)+f(x2)+…+f(xn) |
| n |
(1)试判断y=x2是否为R上的凹函数,并说明理由;
(2)若x、y、z∈R,且x+y+2z=8,试求x2+y2+2z2的最小值并指出取得最小值时x、y、z的值.
考点:进行简单的合情推理
专题:计算题,推理和证明
分析:(1)利用凹函数的定义,即可得出结论;
(2)利用题中条件:“x+y+2z=8”构造柯西不等式:(x2+y2+2z2)(12+12+
2)≥(x+y+2z)2=64这个条件进行计算即可.
(2)利用题中条件:“x+y+2z=8”构造柯西不等式:(x2+y2+2z2)(12+12+
| 2 |
解答:
解:(1)f(
)=(
)2,
=
≥
=(
)2,
∴对任意x1、x2∈(a,b)恒有f(
)≤
成立,
∴y=x2是R上的凹函数;
(2)∵(x2+y2+2z2)(12+12+
2)≥(x+y+2z)2=64,
∴x2+y2+2z2≥16,当且仅当x=y=
z时取等号,
∵x+y+2z=8,∴x=y=4(
+1),z=4+2
.
∴x2+y2+2z2的最小值为16,此时x=y=4(
+1),z=4+2
.
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x12+x22 |
| 2 |
| x12+x22+2x1x2 |
| 4 |
| x1+x2 |
| 2 |
∴对任意x1、x2∈(a,b)恒有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
∴y=x2是R上的凹函数;
(2)∵(x2+y2+2z2)(12+12+
| 2 |
∴x2+y2+2z2≥16,当且仅当x=y=
| 2 |
∵x+y+2z=8,∴x=y=4(
| 2 |
| 2 |
∴x2+y2+2z2的最小值为16,此时x=y=4(
| 2 |
| 2 |
点评:本题考查用综合法证明不等式,关键是利用:(x2+y2+2z2)(12+12+
2)≥(x+y+2z)2=64.
| 2 |

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
如两圆C1:x2+y2=r2与C2:(x-3)2+(y+1)2=r2(r>0)相切,则r的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
9
-(-10)0+(log2
)•(log
2)的值等于( )
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| A、-2 | B、0 | C、8 | D、10 |
 如图,设O为?ABCD所在平面外任意一点,E为OC的中点,若
如图,设O为?ABCD所在平面外任意一点,E为OC的中点,若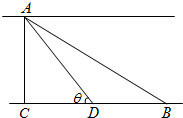 如图,一条河的两岸是平行线,两岸边各有一个小镇A与B,它们的直线距离为2km,河宽AC=1km,根据规划,需要在两岸间铺设一条电缆线,从A处铺设水下电缆到D处(D为线段BC上的点),再从D处铺设地下电缆到B处,已知铺设水下电缆的费用是铺设地下电缆费用的2倍,记∠ADC=θ.
如图,一条河的两岸是平行线,两岸边各有一个小镇A与B,它们的直线距离为2km,河宽AC=1km,根据规划,需要在两岸间铺设一条电缆线,从A处铺设水下电缆到D处(D为线段BC上的点),再从D处铺设地下电缆到B处,已知铺设水下电缆的费用是铺设地下电缆费用的2倍,记∠ADC=θ.