题目内容
已知向量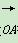 =(λcosα,λsinα)(λ≠0),
=(λcosα,λsinα)(λ≠0),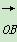 =(-sinβ,cosβ),其中O为坐标原点.
=(-sinβ,cosβ),其中O为坐标原点.
(1)若α-β= 且λ=1,求向量
且λ=1,求向量 与
与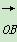 的夹角;
的夹角;
(2)若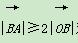 对任意实数α,β都成立,求实数λ的取值范围.
对任意实数α,β都成立,求实数λ的取值范围.

 β都成立,即(λcosα+sinβ)2+(λsinα-cosβ)2≥4对任意实数α,β都成立.
β都成立,即(λcosα+sinβ)2+(λsinα-cosβ)2≥4对任意实数α,β都成立.
整理得λ2+1+2λsin(β-α)≥4对任意实数α,β都成立.
因为-1≤sin(β-α)≤1,
所以
解得λ≥3或λ≤-3.
所以实数λ的取值范围为(-∞,-3]∪[3,+∞)

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
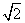 +1,且sinA+sinB=
+1,且sinA+sinB=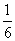 sinC,则角C的大小为( )
sinC,则角C的大小为( )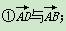
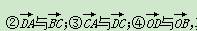 其中可作为这个平行四边形所在平面的一组基底的是( )
其中可作为这个平行四边形所在平面的一组基底的是( )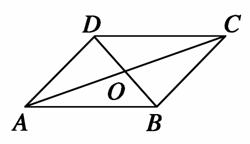
 方向上的投影为( )
方向上的投影为( ) B.
B.
 ,
, =120.
=120.
 求x,y的值.
求x,y的值. ,则|z1+z2|=( )
,则|z1+z2|=( )


 +
+ i是纯虚数,则tan
i是纯虚数,则tan =( )
=( ) B.-7
B.-7 D.-1
D.-1