题目内容
20．已知f（x）是定义在R上周期为4的偶函数，若f（x）在区间[-2，0]上单凋递减，且f（-1）=0，则f（x）在区间[0，10]内的零点个数是5．分析 由题意可得函数图象，数形结合可得．
解答 
解：由题意可得f（1）=f（-1）=0，
函数的图象大致如图所示，
由图象可知f（x）在区间[0，10]内的零点个数为5，
故答案为：5．
点评 本题考查函数的周期性和奇偶性，数形结合是解决问题的关键，属基础题．
练习册系列答案
孟建平名校考卷系列答案
相关题目
10．在年龄互不相同的5名工人中选派工人去看管A、B两个仓库，且两个仓库都至少要有一人看管，若看管仓库A的工人年龄最大的小于看管仓库B的工人年龄最小的，则不同的选派方法有（ ）
| A． | 45 | B． | 49 | C． | 55 | D． | 59 |
11．设F1，F2分别为椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与双曲线C2：$\frac{{x}^{2}}{{{a}_{1}}^{2}}$-$\frac{{y}^{2}}{{{b}_{1}}^{2}}$=1（a1＞b1＞0）的公共焦点，它们在第一象限内交于点M，∠F1MF2=90°，若椭圆的离心率e∈[$\frac{3}{4}$，$\frac{2\sqrt{2}}{3}$]，则双曲线C2的离心率e1的取值范围为（ ）
| A． | [$\frac{2\sqrt{14}}{7}$，$\frac{3\sqrt{2}}{2}$] | B． | [$\frac{2\sqrt{14}}{7}$，$\sqrt{2}$） | C． | [$\sqrt{2}$，$\frac{3\sqrt{2}}{2}$] | D． | [$\frac{3\sqrt{2}}{2}$，+∞） |
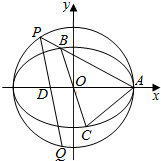如图，在平面直角坐标系xOy中，已知圆O：x2+y2=4，椭圆C：$\frac{x^2}{4}+{y^2}=1$，A为椭圆右顶点．过原点O且异于坐标轴的直线与椭圆C交于B，C两点，直线AB与圆O的另一交点为P，直线PD与圆O的另一交点为Q，其中$D（-\frac{6}{5}，0）$．设直线AB，AC的斜率分别为k1，k2．