ĚâÄżÄÚČÝ
ĄžĚâÄżĄżŇť´ÎżźĘÔÖĐŁŹÎĺΝѧÉúľÄĘýѧŁŹÎďŔíłÉź¨ČçĎÂąíËůĘžŁş

Ł¨1ŁŠŇŞ´Ó5ĂűѧÉúÖĐŃĄ2Č˲ΟÓŇťĎîťîśŻŁŹÇóŃĄÖĐľÄѧÉúÖĐÖÁÉŮÓĐŇťČËľÄÎďŔíłÉź¨¸ßÓÚ90ˇÖľÄ¸ĹÂĘŁť

Ł¨2ŁŠ¸ůžÝÉĎąíĘýžÝŁŹťłöɢľăÍź˛˘ÓĂɢľă͟˾Ă÷ÎďŔíłÉź¨![]() ÓëĘýѧłÉź¨
ÓëĘýѧłÉź¨![]() ÖŽźäĎßĐÔĎŕšŘšŘĎľľÄÇżČőŁŹČçšűžßÓĐ˝ĎÇżľÄĎßĐÔĎŕšŘšŘĎľŁŹÇó
ÖŽźäĎßĐÔĎŕšŘšŘĎľľÄÇżČőŁŹČçšűžßÓĐ˝ĎÇżľÄĎßĐÔĎŕšŘšŘĎľŁŹÇó![]() Óë
Óë![]() ľÄĎßĐԝؚ顽łĚŁ¨ĎľĘýžŤČˇľ˝0.01ŁŠŁťČçšű˛ťžßÓĐĎßĐÔĎŕšŘšŘĎľŁŹÇëËľĂ÷ŔíÓÉ.
ľÄĎßĐԝؚ顽łĚŁ¨ĎľĘýžŤČˇľ˝0.01ŁŠŁťČçšű˛ťžßÓĐĎßĐÔĎŕšŘšŘĎľŁŹÇëËľĂ÷ŔíÓÉ.
˛ÎżźšŤĘ˝Łş
ťŘšéÖąĎ߾ġ˝łĚĘÇ![]() ŁŹĆäÖĐ
ŁŹĆäÖĐ ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ
![]() ĘÇÓë
ĘÇÓë![]() śÔÓŚľÄťŘšéšŔźĆÖľŁŹ
śÔÓŚľÄťŘšéšŔźĆÖľŁŹ
˛ÎżźĘýžÝŁş ![]() ŁŹ
ŁŹ ![]() .
.
Ąž´đ°¸Ąż(1) ![]() Łť(2)´đ°¸źű˝âÎö.
Łť(2)´đ°¸źű˝âÎö.
Ąž˝âÎöĄżĘÔĚâˇÖÎöŁş
(1)ÓÉĚâŇâÁĐłöËůÓĐżÉÄÜľÄĘÂźţŁŹ˝áşĎšĹľä¸ĹĐÍźĆË㚍ʽżÉľĂÖÁÉŮÓĐŇťČËľÄÎďŔíłÉź¨¸ßÓÚ90ˇÖľÄ¸ĹÂĘÎŞ![]() Łť
Łť
(2)ťćÖĆɢľăÍźŁŹšŰ˛ěżÉľĂÎďŔíłÉź¨ÓëĘýѧłÉź¨¸ßśČŐýĎŕšŘ.˝áşĎĎßĐԝؚ顽łĚľÄźĆË㚍ʽżÉľĂŁşĎßĐԝؚ顽łĚÎŞ![]() .
.
ĘÔĚâ˝âÎöŁş
(1)´Ó5ĂűѧÉúÖĐČÎČĄ2ĂűѧÉúľÄËůÓĐÇéżöÎŞŁş(A1ŁŹA2)ŁŹ(A1ŁŹA3)ŁŹ(A1ŁŹA4)ŁŹ(A1ŁŹA5)ŁŹ(A2ŁŹA3)ŁŹ(A2ŁŹA4)ŁŹ(A2ŁŹA5)ŁŹ(A3ŁŹA4)ŁŹ(A3ŁŹA5)ŁŹ(A4ŁŹA5)ŁŹš˛10ÖÖÇéżö.
ĆäÖĐÖÁÉŮÓĐŇťČËľÄÎďŔíłÉź¨¸ßÓÚ90ˇÖľÄÇéżöÓĐŁş
(A1ŁŹA2)ŁŹ(A1ŁŹA4)ŁŹ(A2ŁŹA3)ŁŹ(A2ŁŹA4)ŁŹ(A2ŁŹA5)ŁŹ(A3ŁŹA4)ŁŹ(A4ŁŹA5)š˛7ÖÖÇéżöŁŹ
šĘŃĄÖĐľÄѧÉúÖĐÖÁÉŮÓĐŇťČËľÄÎďŔíłÉź¨¸ßÓÚ90ˇÖľÄ¸ĹÂĘÎŞ![]() .
.
(2)
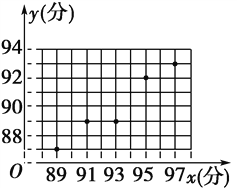
żÉŇÔż´łöŁŹÎďŔíłÉź¨ÓëĘýѧłÉź¨¸ßśČŐýĎŕšŘ.ɢľăÍźČçÍźËůĘžŁş
´ÓɢľăÍźżÉŇÔż´łöŐâĐŠľă´óÖ¡ֲźÔÚŇťĚőÖąĎ߸˝˝üŁŹ˛˘ÇŇÔÚÖđ˛˝ÉĎÉýŁŹšĘÎďŔíłÉź¨ÓëĘýѧłÉź¨ŐýĎŕšŘ.
ÉčyÓëxľÄĎßĐԝؚ顽łĚĘÇ![]() Ł˝
Ł˝![]() xŁŤ
xŁŤ![]() ŁŹ¸ůžÝËů¸řľÄĘýžÝŁŹżÉŇÔźĆËăłö
ŁŹ¸ůžÝËů¸řľÄĘýžÝŁŹżÉŇÔźĆËăłö
![]() Ł˝93ŁŹ
Ł˝93ŁŹ![]() Ł˝90,
Ł˝90,
![]() Ł˝
Ł˝![]() Ł˝0.75ŁŹ
Ł˝0.75ŁŹ![]() Ł˝90Ł0.75ĄÁ93Ł˝20.25ŁŹ
Ł˝90Ł0.75ĄÁ93Ł˝20.25ŁŹ
ËůŇÔyÓëxľÄĎßĐԝؚ顽łĚĘÇ
![]() Ł˝0.75xŁŤ20.25.
Ł˝0.75xŁŤ20.25.





