题目内容
已知y=f(x)为二次函数,若y=f(x)在x=2处取得最小值-4,且y=f(x)的图象经过原点,则函数y=f(log
x)在区间[
,2]上的最大值为 .
| 1 |
| 2 |
| 1 |
| 8 |
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:利用待定系数法求二次函数的解析式,根据对数函数的单调性和二次函数的性质进行求值.
解答:
解:设二次函数f(x)=a(x-2)2-4,
∵函数图象过原点,
∴f(0)=0,解得a=1,
∴f(x)=(x-2)2-4.
∵x∈[
,2],∴log
x∈[-1,3],设t=log
x,则t∈[-1,3],
则g(t)=(t-2)2-4.且t∈[-1,3],
∴当t=-1,即x=2时,函数y有最大值5.
故答案为:5
∵函数图象过原点,
∴f(0)=0,解得a=1,
∴f(x)=(x-2)2-4.
∵x∈[
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
则g(t)=(t-2)2-4.且t∈[-1,3],
∴当t=-1,即x=2时,函数y有最大值5.
故答案为:5
点评:本题主要考查二次函数的图象和性质以及对数函数的基本运算,利用换元法将条件转化为二次函数是解决本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
若 a>b,则下列不等式正确的是( )
| A、a2>b2 |
| B、ab>ac |
| C、a-c>b-c |
| D、ac2>bc2 |
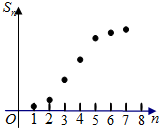 某工厂前n年的总产量Sn与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高.m值为( )
某工厂前n年的总产量Sn与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高.m值为( )| A、2 | B、4 | C、5 | D、8 |
设等比数列{an}的前n项和为Sn,若S10:S5=1:2,则
=( )
| S5+S10+S15 |
| S10-S5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知直线l:3x-y+6=0,则直线l在x轴上的截距是( )
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
| D、-2 |