题目内容
4.给出下列四个命题:①三点确定一个平面;
②三条两两相交的直线确定一个平面;
③在空间上,与不共面四点A,B,C,D距离相等的平面恰有7个;
④两个相交平面把空间分成四个区域.
其中真命题的序号是③④(写出所有真命题的序号).
分析 ①根据平面的公理“三点定面”即可判断命题错误;
②根据三条两两相交的直线可能不共面,即可判断命题错误;
③根据空间四点不共面时,四点构成一个三棱锥,讨论平面一侧有一点,另一侧有三点时,和平面一侧有两点,另一侧有两点时,满足条件的平面数是多少即可;
④根据实际情况即可得出结论正确.
解答 解:对于①,不在同一直线上的三点确定一个平面,∴①错误;
对于②,不共点的三条两两相交的直线确定一个平面,∴②错误;
对于③,空间四点A、B、C、D不共面时,则四点构成一个三棱锥,如图: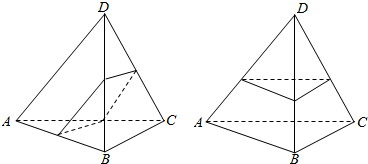
当平面一侧有一点,另一侧有三点时,令截面与四棱锥的四个面之一平行,第四个顶点到这个截面的距离与其相对的面到此截面的距离相等,这样的平面有4个,
当平面一侧有两点,另一侧有两点时,即过相对棱的异面直线公垂线段的中点,且和两条相对棱平行的平面,满足条件.因三棱锥的相对棱有三对,则此时满足条件的平面个数是3个,
所以满足条件的平面恰有7个,③正确;
对于④,两个相交平面把空间分成四个区域是真命题,∴④正确.
综上,正确的命题序号是③④.
故答案为:③④.
点评 本题考点平面的基本性质与推论的应用问题,也考查了空间图形的结构特征,解题的关键是熟练掌握平面的基本性质及公理,从而作出判断,是基础题目.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
15.在空间坐标系O-xyz中,已知点A(2,1,0),则与点A关于原点对称的点B的坐标为( )
| A. | (2,0,1) | B. | (-2,-1,0) | C. | (2,0,-1) | D. | (2,-1,0) |
9.(x2+x+y)5的展开式中,x7y的系数为( )
| A. | 10 | B. | 20 | C. | 30 | D. | 60 |
13.下列函数中,导数不等于$\frac{1}{2}$sin2x的是( )
| A. | 2-$\frac{1}{4}$cos2x | B. | 2+$\frac{1}{2}$sin2x | C. | $\frac{1}{2}$sin2x | D. | x-$\frac{1}{2}$cos2x |
14.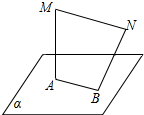 如图,MA⊥平面α,AB?平面α,BN与平面α所成的角为60°,且AB⊥BN,MA=AB=BN=1,则MN的长为( )
如图,MA⊥平面α,AB?平面α,BN与平面α所成的角为60°,且AB⊥BN,MA=AB=BN=1,则MN的长为( )
 如图,MA⊥平面α,AB?平面α,BN与平面α所成的角为60°,且AB⊥BN,MA=AB=BN=1,则MN的长为( )
如图,MA⊥平面α,AB?平面α,BN与平面α所成的角为60°,且AB⊥BN,MA=AB=BN=1,则MN的长为( )| A. | $\sqrt{3+\sqrt{3}}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3-\sqrt{3}}$ |
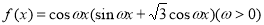 ,如果存在实数
,如果存在实数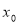 ,使得对任意的实数
,使得对任意的实数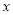 ,都有
,都有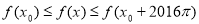 成立,则
成立,则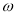 的最小值为( )
的最小值为( )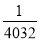 B.
B.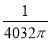 C.
C. D.
D.